基于夏普比的CTA筛选指标

作者：净值还在水上

题图：净值还在水上微信公众号

本文首先从简单的夏普比开始，解释传统夏普的局限性，然后介绍两个改进指标，

• Probabilistic Sharpe Ratio（PSR）
• Generalized Sharpe Ratio（GSR）

这两种方法不仅考虑了净值的收益和波动，还考虑了回报的分布特性，如偏度和峰度，即使在超额回报为负的情况下也适用。

夏普的局限性

夏普比（Sharpe Ratio，简称SR）是一种衡量投资风险调整后收益的指标，被广泛应用于评估投资策略的表现。然而，夏普比存在几个局限性：

• 正态分布假设：夏普比假设收益率是正态分布的。这意味着收益率的分布是对称的，并且大多数收益会集中在平均值附近。然而，现实中的收益率分布可能并不符合这一假设，特别是当市场出现极端情况或尾部风险时；
• 波动性衡量：夏普比的分母是收益率的标准差，它将收益率高于或低于平均值的变化视为同等重要。然而，风险厌恶的投资者可能更关心下行风险而非整体波动性；
• 负回报问题：当回报为负时，夏普比可能会产生反直觉的结果。即使两个投资的收益相同，波动性更高的投资反而会有一个更高的夏普比；
• 尾部风险未考虑：夏普比没有考虑到收益率分布的尾部风险，这可能导致对投资策略风险的低估；
• 非正态分布的影响：即使收益率分布是非正态的，夏普比的估计值仍然遵循正态分布，但估计的标准差会受到收益率分布的偏度和峰度的影响。

Probabilistic Sharpe Ratio（PSR）

基于SR的这些性质，Marcos Lopez de Prado提出Probabilistic Sharpe Ratio（PSR），试图通过考虑回报分布的偏度（skewness）和峰度（kurtosis）来解决传统夏普的局限性。

Generalized Sharpe Ratio（GSR）

接下来，我们介绍Generalized Sharpe Ratio，它从效用函数的角度出发，将更高阶的moments纳入指标设计，且在收益率正态分布的情况下与传统夏普的效果相同。

正态分布下的效用最大化

非正态分布

结合PSR与GSR的CTA筛选

• 第一步：利用PSR进行策略筛选，通过对累积分布函数求逆，我们可以计算每个策略，当PSR=0.95时，对应的目标夏普比，并进行排序。注意越小，CTA产品的超额能力越强；
• 第二步：计算GSR，对应以上三元一次方程的解；
• 第三步：根据对CTA产品进行降序排列，根据GSR进行升序排列。
• 当然这两个指标有多种结合方法，例如对每个指标的top10取交集，可以得到以下几个产品。它们的收益相对更高，涨跌更加均匀，尾部行情更少见，且夏普要高于市场平均水平。

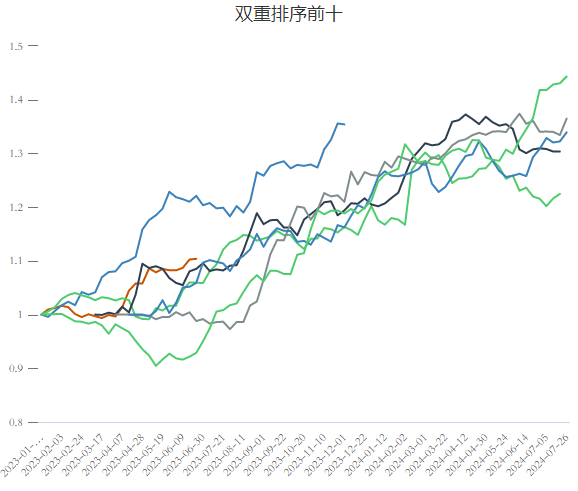
参考资料

• Marcos López de Prado and David Bailey (2012) “The Sharpe ratio efficient frontier”
• Mertens, E. (2002) “Variance of the IID estimator in Lo (2002)”

版权声明：文章版权归原作者所有，部分文章由作者授权本平台发布，若有其他不妥之处的可与小编联系。