作者:大象咖啡屋
题图:大象咖啡屋微信公众号
正文
我们在上一篇笔记“漫谈全天候(中):分散、顺周期与持仓比例”中,通过人为的方式探索了不同持仓比例下的组合表现。我们同时谈到,全天候策略的一个核心思想就是分散风险(一定程度牺牲收益)。分散风险不代表均分持仓比例、使不同资产的持仓一致,同样比例的权益资产风险必然要比固收资产高很多。我们要做到的是使所有资产的风险贡献一致。基于这种思路下的配置策略就是风险平价(risk parity)。
风险平价策略最初被磐安(Pan Agora)基金的首席投资官钱恩平(Edward Qian)提出。桥水的全天候基金有没有用到该策略,其实并没有确切依据。我相信是借鉴了,但达里奥多次表示桥水内部有自己的一整套风险控制模型。
本篇笔记我们着重探讨风险平价模型应用于全天候策略的表现。因风险平价模型涉及较多数理统计的知识,在文章前半部分包含有较多公式和理论介绍,不熟悉的小伙伴可直接跳到第3节阅读该模型的实证结果。
1、风险度量
收益率衡量资产价格在某段时间内的变化程度。一种简单的计算方式是如下的算术收益率:

金融工程中则更多使用如下的对数收益率:
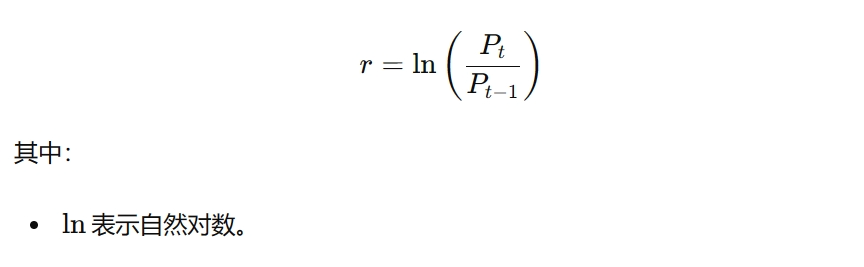
对数收益率在多期复利计算的场景下更为实用,并且解决了算术收益率在较大波动下的非对称性问题。
如果收益率的变动接近0,说明资产的确定性极高,那么风险相对就低;反之收益率变动较大,那么不确定性就增大,风险也就加大。因此,通常采用收益率的变动程度度量风险,具体而言,使用收益率(在某一区间的)标准差。

sigma就是我们用来度量风险的指标。
出于比较过程一致的目的,通常将波动率进行年化,如果已知周期性波动率(例如,日波动率、月波动率),年化波动率计算公式为:

波动率具有聚簇效应和均值回归的特性。聚簇效应是指高波动后大概率仍是高波动;低波动后大概率仍是低波动。均值回归是指,一段时间的高波动后总会向低波动回归,反之长时间的低波动之后也会出现高波动。
2、风险平价
上一节中利用收益率的标准差可以度量单个资产的风险,如果组合中有多个资产,又如何来度量组合的风险呢?通常,组合的风险定义如下:

上述定义方式,不仅考虑了单个资产自身的波动,还考虑了多个资产之间的相关性。
我们的目的就是确定权重向量w,使得组合中资产的风险贡献一致。为此,还需要定义每个资产对于组合的边际风险贡献和总体风险贡献。
定义1:资产i的边际风险(MRC,Marginal Risk Contribution)

资产i的边际风险贡献定义为组合风险对资产i权重的偏导数,也就是资产i权重的微小变化所引起的组合风险的变化。基于边际风险贡献可以定义出资产i对组合风险的贡献量,如下。
定义2:资产i的风险贡献(RC,Risk Contribution)

风险平价条件
有了组合中每个资产对组合整体风险的贡献度量,按照我们最初的目标,使得所有资产的风险贡献一致,那么可以得到风险平价的理论条件如下:
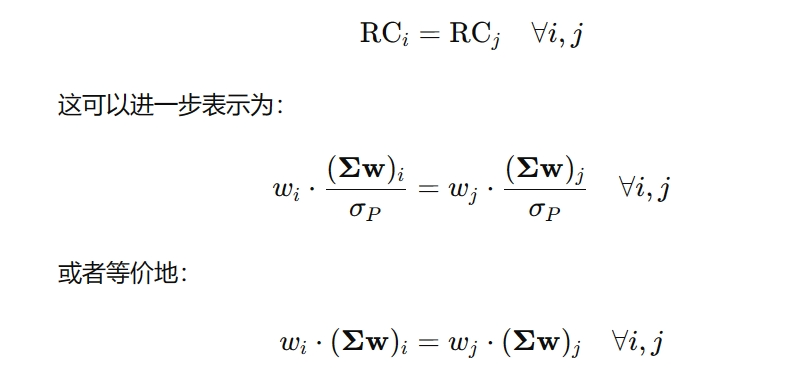
计算步骤
实际中,可能并不存在一组权重使得所有资产的风险贡献正好一样,我们会将寻找这组权重的过程转换为一个非线性的优化问题。具体计算步骤如下:
步骤一:计算协方差矩阵,使用资产的历史收益率数据(比如过去20日的日收益率)计算协方差矩阵。
步骤二:选择初始权重w,比如所有资产等权。
步骤三:调整权重,求解下面目标函数的最优解,使得每个资产的风险贡献接近相等。
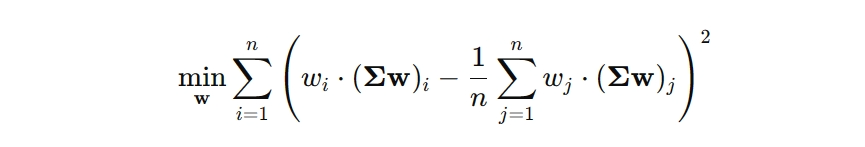
求解上述函数的最优解可以采用牛顿法或者梯度下降的方法。
步骤四:归一化上一步骤得到的权重,使得权重和为1。
实际应用中还需做如下调整:
(1)杠杆调整:由于不同资产的波动率不同,可能需要对低波动率资产(如债券)使用杠杆,以实现风险平价目标。
(2)动态调整:市场条件和资产的风险特征会随着时间变化,因此需要定期重新计算和调整投资组合权重,以保持风险平价状态。
实现上使用python的scipy库,核心代码如下:
import numpy as np
from scipy.optimize import minimize
def calculate_cov(R):
"""计算协方差
R 为 二维向量n*m, n是n个资产, m是序列点数
"""
data = np.array(R)
return np.cov(data)
def calculate_portfolio_risk(w, cov):
"""根据资产权重计算目前组合风险
w: 是当前的资产权重向量, 为list,
cov: 是协方差矩阵
"""
w = np.matrix(w)
return np.sqrt((w*cov*w.T)[0, 0])
def calculate_risk_contribution(w, cov):
"""根据资产权重计算目前每个资产的总风险贡献
w: 是当前的资产权重向量, 为list,
cov: 是协方差矩阵
"""
w = np.matrix(w)
sigma_p = calculate_portfolio_risk(w, cov)
MRC = cov*w.T
RC = np.multiply(MRC, w.T)/sigma_p
return RC
def risk_budget_objective(w, pars):
"""风险评价优化目标函数
w: 是当前的资产权重向量, 为list
pars[0]: # 协方差矩阵
pars[1]: # 资产风险贡献目标比例
"""
cov = pars[0]
x_t = pars[1]
# 根据资产权重计算目前组合风险
sigma_p = calculate_portfolio_risk(w, cov)
# 根据资产权重计算目前每个资产的总风险贡献
RC = calculate_risk_contribution(w, cov)
# 根据资产风险贡献目标比例计算每个资产的风险贡献
RC_target = np.asmatrix(np.multiply(sigma_p, x_t))
# 计算目前的总风险贡献与目标的总风险贡献的差值
loss = sum(np.square(RC-RC_target.T))[0, 0]
# 输出loss太小了,人为放大
return loss*1e5
def total_weight_constraint(x):
return np.sum(x)-1.0
def long_only_constraint(x):
return x
def run_computing_best_w(x, cov):
"""根据每个资产的目标风险贡献度来计算各资产的比重
x:资产的目标贡献度向量,和应该是1,比如[0.25, 0.25, 0.25, 0.25]
cov: 协方差矩阵
"""
# 初始权重设为等权
w_0 = np.array([1/len(x) for _ in x])
x_t = np.array(x)
cons = [
{'type': 'eq', 'fun': total_weight_constraint},
{'type': 'ineq', 'fun': long_only_constraint},
]
res = minimize(risk_budget_objective, w_0, args=[cov, x_t],
method='SLSQP',
constraints=cons,
options={'disp': True}
)
w_rb = np.asmatrix(res.x)
return w_rb
if __name__ == '__main__':
pass3、实证结果
我们通过回测实验来给出风险平价策略的实证结果。
标的
实验中所使用的标的和前两篇笔记一致,均为如下国内市场上市ETF基金:
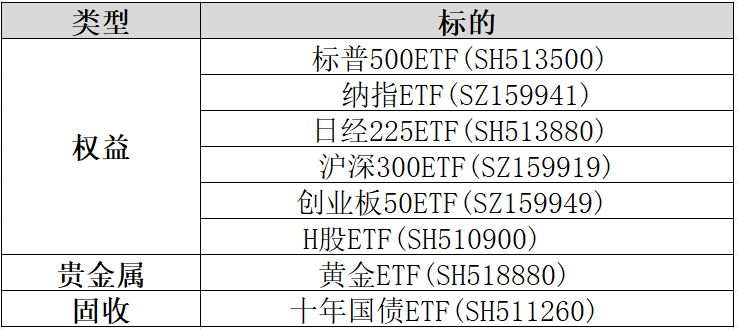
所有标的分为权益(6只ETF)、贵金属(1只黄金ETF)以及固收(1只ETF)。
收益率序列窗口
在上一节中,我们知道计算某一个时间点各资产对组合的风险贡献时,需要所给定资产的日收益率序列。在此我们选择20个交易日作为日收益率序列的窗口大小。太短的窗口不足以捕捉趋势性的波动;太长的窗口容易造成钝化。
确定好窗口大小后,我们可以计算出每个时间点位各资产的权重占比,所示如下图。
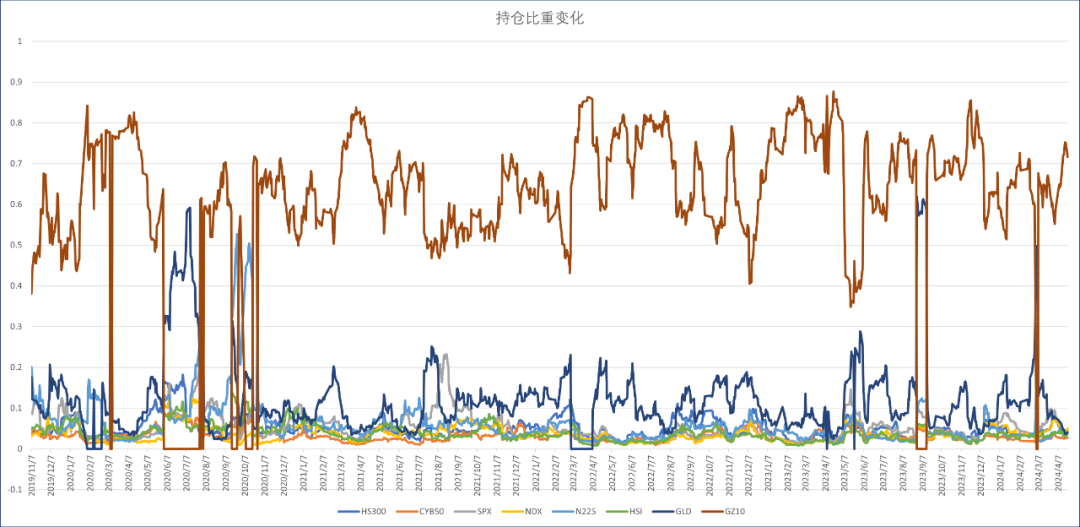
上图中,褐色曲线是国债ETF的占比变化,可以看到在0.5与0.9之间波动,始终作为第一大权重资产;第二大权重资产基本上都是蓝色曲线的黄金;其他颜色的曲线都是各个权益资产的占比变化。曲线中有一些权重变化的脉冲,比如2020年3月初以及2020年6月到8月初,国债ETF的权重降为0。彼时权益市场恢复,经济面向好,大资金调仓导致债券资产的大幅波动导致的。类似的,2022年底也发生了较大的债券资产回撤。因为国债的占比较大,所以它的权重波动就会造成比较大的影响。而它的权重降低之后,其他的资产权重就会被迫抬升。在实际中,短期内不会进行如此大的持仓比例切换。
这里有两个深入研究的切入点:(1)收益率序列窗口大小;(2)可以尝试用不同周期的收益率作为序列数值,这里实验是日收益率,也可以采用周收益率或月度收益率。
实验配置
与上篇笔记保持一致,回测区间仍旧是2019年10月11日至2024年4月22日。初始资金100万,手续费为双向万五,滑点统一为每份0.02。
回测过程进行定期再平衡,实验查看分别在20、30、60、120和250个交易日再平衡持仓比例的回测效果。各比例的净值对比如下:
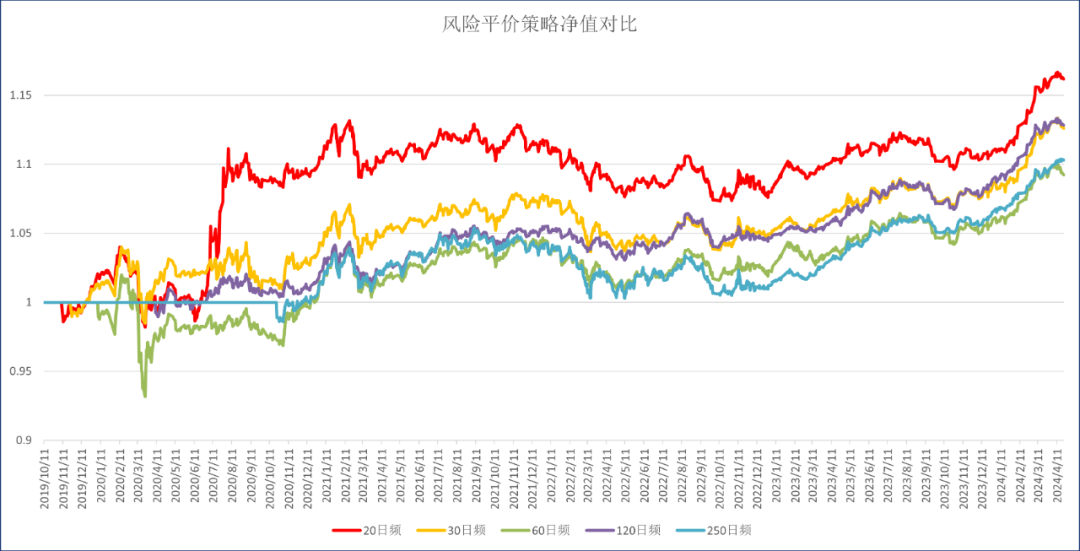
具体的统计数据对比如下:

上图净值图中,红色曲线是20日调仓频率,在2020年6月到7月,净值有一个跳涨,原因就是上面说到的,固定资产仓位降为0,权益资产仓位被迫抬升,而彼时权益资产从疫情低谷开始反弹,表现确实不错,不过此后有长达两年多的盘整过程;其他调仓频率正好避开了固收资产仓位的脉冲变化。在所有调仓频率下,120日频率的净值曲线相对而言拿着比较舒服。不过,令人沮丧的是,所有调仓频率下策略表现都不佳,夏普比都没有超过1,甚至还有负的(说明还不如无风险资产),卡玛比率也并不亮眼;除了20日频的跳涨,其它频率下的年化收益都没超过3%。
从实证结果来看,风险平价策略并没有非常令人激动的结果。具体原因分析如下:
(1)此类策略一个比较大的问题肯定就是滞后性,也就是说我们在某个时间点算出来的波动率,或者算出来的风险,只是过去一段时间的风险度量,并不能代表未来的风险。
(2)另外,风险平价本质上是一个满仓策略,也就是说当某个资产波动比较大的时候,它的仓位会降低,那么会导致其他资产仓位被动抬升。但是如果所有资产的风险都在抬升的话,那整个组合的总体风险不可避免会增加。
(3)风险平价策略是纯数学模型,在使用时,并没有考虑到实际的宏观环境,仅仅根据资产前一阶段风险表现做出决策。这种决策过于微观,只窥一斑,未见全豹。实际应用中,更多地是结合多维度的分析,从宏观到微观,然后做出综合的判断。
4、结语
本篇笔记介绍了风险平价策略,回测实验并未带来乐观的结果,但也不代表我们应完全放弃风险平价策略。我们可以在如下方面作进一步研究:
(1)深入研究模型中的假设条件。比如收益率窗口的选取、收益率的计算周期、再平衡的窗口大小等。
(2)纳入更多样的资产类型。风险平价策略只能平衡风险,并不能降低组合的整体风险,所以是否可以在组合中加入更多的负相关资产,比如现金类资产或者另类资产等。
(3)结合更多维度的数据。将风险平价模型算出来的风险分配方案结合更多维度的数据进行综合判断,比如对于未来的宏观环境分析、经济或行业政策分析等。
相信通过上述层面的深入研究,可以发现更多有价值的信息。
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
