作者：因子动物园
题图：因子动物园个人微信公众号
1. Delta-hedged option returns
在展开具体讨论之前，有必要首先对期权因子研究的对象及其计算做一说明。在股票因子研究中，我们直接以股票（超额）收益为预测对象。但对于期权因子研究，则不能简单地用期权收益作为预测对象。原因也很直观：期权收益会受到底层股票收益的显著影响，且由于期权天然带杠杆，因此，股票收益的较小变动都可能使得期权收益发生极大的变化。因此，为了理解除股票收益之外的期权收益驱动因素从而构建期权因子，就需要剥离掉股票收益的影响。Delta-hedge 也就非常自然了。
由于期权的 Delta 代表期权价格对股票价格的敏感性，理论上，Delta-hedged 后的期权收益就不再受股票价格变动的影响。当然，严格的 Delta-hedge 需要连续进行对冲，在实践中这通常是不现实的。在期权因子的研究中，则往往采取按日调整的方式进行对冲，可以基本保证对冲后的期权收益不受股票价格波动的影响。
进一步，为计算 Delta-hedged 期权收益，首先参照 Cao and Han (2013)的做法，按照如下方式进行计算 Delta-hedged 期权的利润：
2. 异质波动率因子
有了 Delta-hedged 期权收益的表达式，便可进入本文的正题，考察期权因子的构造及表现。
首先来看一个代表性因子：股票异质波动率（IVOL）。之所以选择异质波动率因子，一方面，异质波动率我们已经非常熟悉。另一方面，异质波动率因子是较早提出的期权因子之一，由 Cao and Han (2013) 提出。这篇文章的写作也非常清晰、规范，是很好的写作模板。
Cao and Han (2013) 认为，期权市场中也存在异质波动率效应，即对于那些异质波动率较高的股票的期权，其 Delta-hedged 期权收益会显著更低。
为实证检验这一论点，在其主要分析中，Cao and Han (2013) 为每只股票仔细筛选了最接近平值（at-the-money）的看涨期权，并要求期权在到期日之前不会除权。作者还剔除了那些价格显著违背看涨看跌期权平价关系的期权。此外，为排除微观噪声的影响，还依据交易量、买卖报价等做了进一步的过滤。
表 1 展示了其基准结果。Panel A 表明，利用不同方法估计股票波动率，都能发现 Delta-hedged 期权收益与股票波动率之间存在显著的负相关关系。Panel B 进一步将波动率拆分为异质波动率（标准算法：前一月的股票日度超额收益对 Fama-French 三因子模型回归的残差的标准差）和系统性波动率（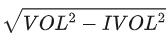
），结果表明期权收益与股票波动率的负向关系主要由 IVOL 所驱动，而系统性波动率与期权收益的关系实际上是显著为正的。采用月度数据估计波动率，或依据 GARCH(1, 1) 模型来估计预期 IVOL，结果也非常稳健。
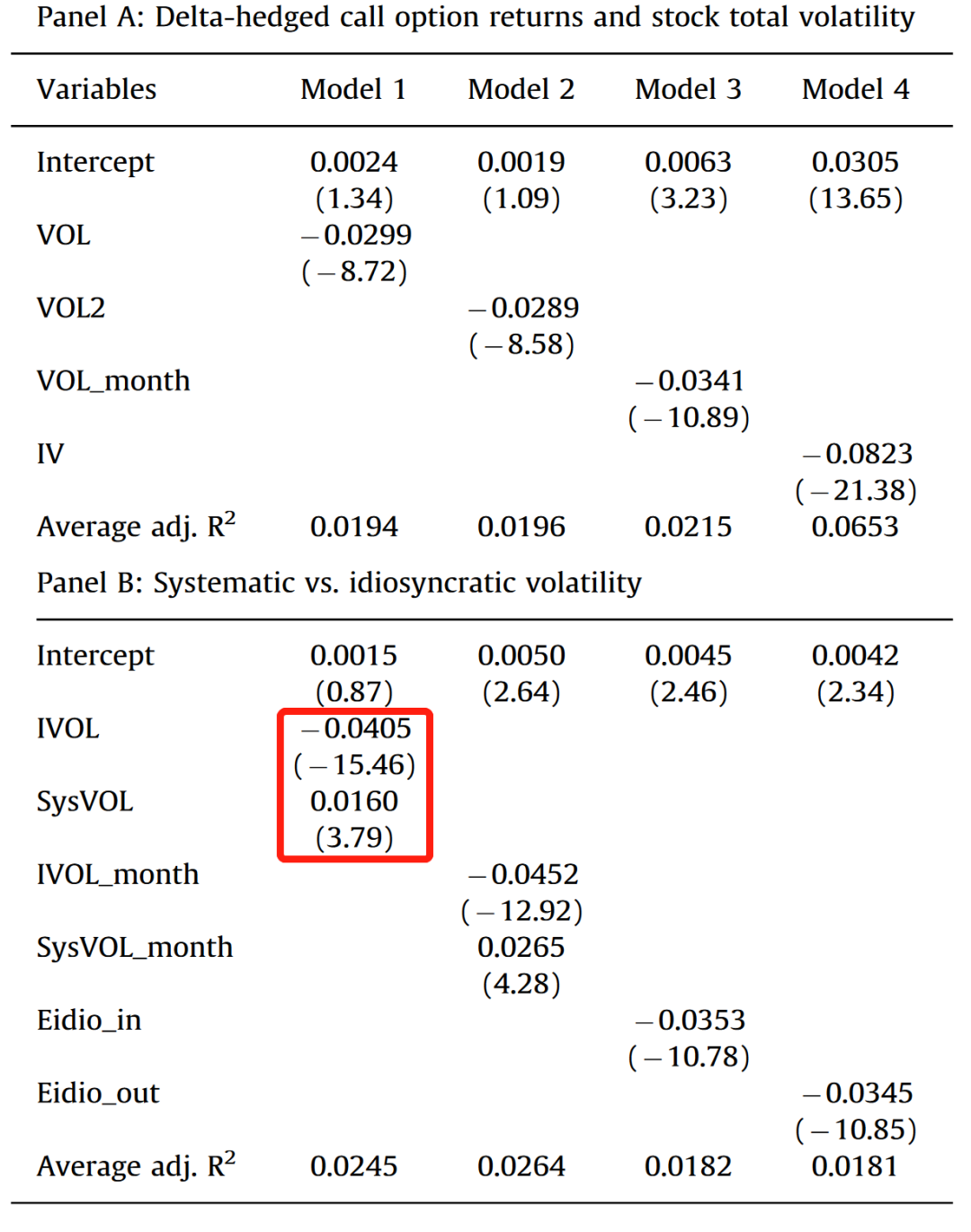
表 1：股票波动率与 Delta-hedged 期权收益. 数据来源：Cao and Han (2013).
为理解上述发现，Cao and Han (2013) 着重强调了受到约束的中介机构的作用，而这本质上与套利限制（litmits-to-arbitrage）有关。具体来看，高 IVOL 股票的期权可能吸引更多的投机者，也使得卖出这些期权的中介机构更加难以对期权进行有效的对冲。为此，中介机构需要额外的补偿才有动机承担相关的风险。这使得高 IVOL 股票的期权价格上升，从而显著降低了其预期收益。
沿着这一思路，代表套利限制的代理变量也应对 Delta-hedged 期权收益有显著影响，且控制这些变量可能有助于缓和期权收益与 IVOL 的负相关性。Cao and Han (2013) 进一步的实证分析表明的确如此。其中尤其重要的套利限制因素/代理变量是股票的流动性（用经典的 Amihud illiquidity measure 代表）和股票价格：流动性越差、市值越小，Delta-hedged 期权收益也越低。而控制这些因素后，IVOL 对 Delta-hedged 期权收益的影响则显著下降（系数从 -0.0405 下降至 -.0233），但仍然显著。换言之，套利限制有助于解释 Delta-hedged 期权授予与股票 IVOL 之间的负相关性，但并不能完全解释这一发现。
Cao and Han (2013) 还考虑了诸多其他可能性。例如，这一发现是否来自于与波动率有关的期权定价偏误等原因。其实证分析表明结果是非常稳健的。您如果对相关细节感兴趣，可找原文自行阅读。
3. 期权收益预测与因子模型
以异质波动率因子为代表介绍了期权（单）因子研究后，接下来我们来看如何利用期权及股票特征对期权收益的预测以及如何构建简约的期权因子模型。
借鉴 Gu et al. (2020) 关于用机器学习方法预测股票收益的经典研究，Bali et al. (2023) 这篇 RFS forthcoming 的文章考察了用机器学习方法和大量期权与股票特征来预测期权收益的可行性。值得注意的是，考察机器学习方法对期权收益的预测能力的 motivation 并不仅仅是简单的方法应用。其核心在于由于期权本身的特征，Delta-hedged 期权收益与期权及股票特征之间可能存在显著的非线性关系，且非线性的重要性可能远高于股票。而机器学习方法则有助于更好地捕捉这一非线性关系。
具体来看，参照 Gu et al. (2020)，作者考察了十余种常见机器学习方法。而在预测特征方面，Bali et al. (2023) 构建了一个非常丰富的特征库，其中包括 80 种期权特征、94 种股票特征，90 个行业虚拟变量（dummy variables），以及已有文献发现的其他可能有助于预测 期权收益的特征，如违约风险。
图 1 展示了其主要结果。不考虑集成学习方法（ensemble methods），表现最好的单一方法是 GBR，即梯度提升回归，这是一种典型的非线性方法。值得注意的是，与作者的猜想一致，线性模型的表现不佳，无论是惩罚回归（Ridge/Lasso/Elastic Net），还是主成分回归（PCR）和偏最小二乘（PLS），样本外 都是负的。基于线性模型的集成学习方法（L-En）有正的样本外 ，但仍显著低于非线性方法。
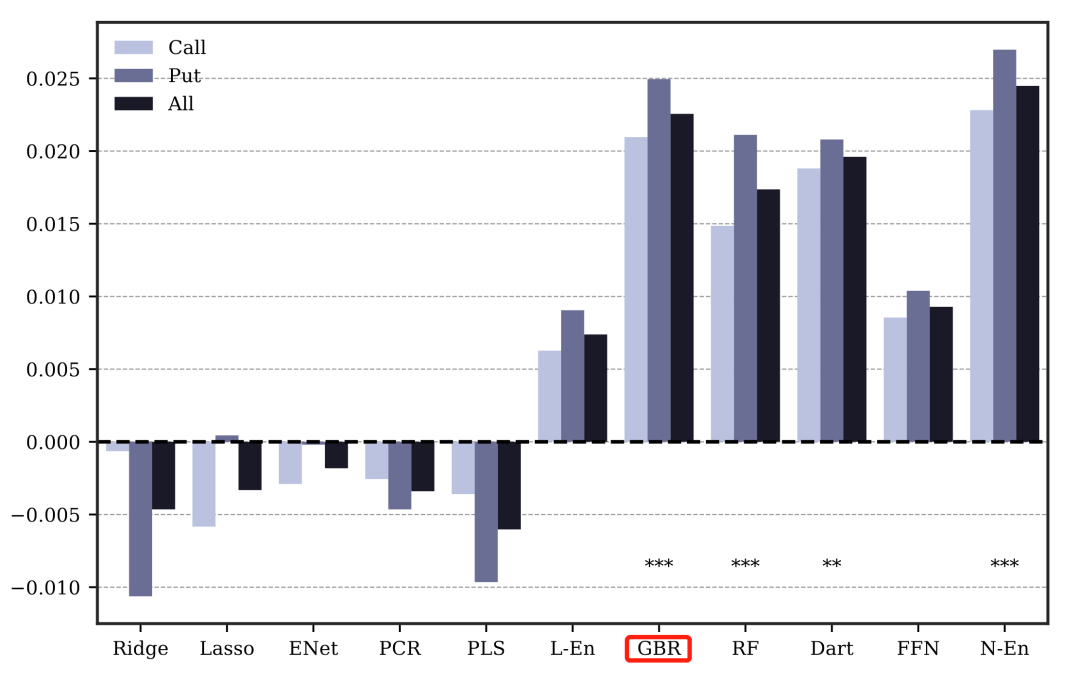
图 1：不同机器学习丰富的样本外 . 数据来源：Bali et al. (2023).
有鉴于此，期权因子模型中大概也应该包含能考虑非线性特征或关联的因子。实证资产定价中的两位扛把子 Bryan Kelly 和前文提及的 Turan Bali，各自与合作者做了一个期权因子模型。
先来看 Büchner and Kelly (2022) 的三因子模型。其出发点是，由于期权价格和特征往往会快速变化，这往往会导致期权的因子暴露在短期内发生迅速变化，因此，需要充分考虑 conditional factor exposures. 自然地，Kelly, Pruitt and Su (2020) 提出并在 Kelly 的多篇顶刊论文中已成功应用的工具 PCA (Instrumented PCA, IPCA) 方法便再合适不过。
但需要注意的是，Büchner and Kelly (2022) 聚焦在 S&P 500 股指期权、而非个股期权上。他们利用 IPCA 方法构造了一个三因子模型，这个模型可以解释 S&P 500 股指期权超过 85% 的收益变化。有趣的是，这一三因子模型还可与经济直觉关联起来，大体可以对应经典的水平（level）、斜率（slope）和偏度（skew）。
Bali et al. (2022) 则与本文介绍的其他研究类似，聚焦于个股期权，并提出了一个包括了多个非线性特征的期权定价模型。与前述 Bali et al. (2023) 关于期权收益预测的研究不同，Bali et al. (2022) 并非用机器学习方法从数据中提取非线性因子，而是采取了更符合经济学、金融学传统研究的方式：首先从理论上推导预期 Delta-hedged 期权收益同期权和股票特征之间的关系，进而按照理论关系构建因子和因子模型。
具体来看，利用测度变换和一些数学推导，Bali et al. (2022) 证明，预期 Delta-hedged 期权收益可以分解为以下两个部分：
- 第一部分是期权隐含的股票波动率、偏度和峰度同股票实际特征之间的差异（即隐含的超额二、三、四阶矩）；
- 第二部分则是期权价格、股票价格以及股票的市场 beta 的一个高度非线性的函数。由于期权价格与股票价格高度相关，因此作者只保留了期权价格；此外，鉴于低价资产往往也有着很差的流动性，而已有研究表明期权流动性对期权收益有显著的影响，因此，作者额外加入了期权流动性因子。
综上，Bali et al. (2022) 构建了一个六因子模型（OPT6），这六个因子可分为三个部分：1）期权市场因子；2）期权隐含的股票波动率、偏度和峰度与实际值的差异；3）期权价格和流动性。除偏度相关因子以外，其余 5 个因子的月均收益都超过了 1%，且高度显著。
最为核心的结果自然是对期权收益的解释能力。Bali et al. (2022) 表明其 OPT6 模型对期权异象组合收益的解释力显著优于各类传统因子模型，同样也优于 BK 的期权因子模型。表 2 报告了不同因子模型对期权异象组合的解释力。以 Panel A 为例，当仅考虑 35 个基于期权特征构建的异象时，有 30 个异象的原始超额收益显著，月均 alpha 绝对值高达 1.63%；而当考察相对于 OPT6 模型的 alpha 时，则仅有 2 个异象显著，月均 alpha 绝对值下降至 0.39%，远低于原始水平和相对于其他因子模型的 alpha 绝对值均值。从模型的拟合优度也可见，OPT6 模型的拟合要显著优于其他候选模型。值得注意的是，前述 BK 模型对于股票期权异象也几乎没有解释力，可见 OPT6 模型和 BK 模型在关注点和表现上有着很大的差异。
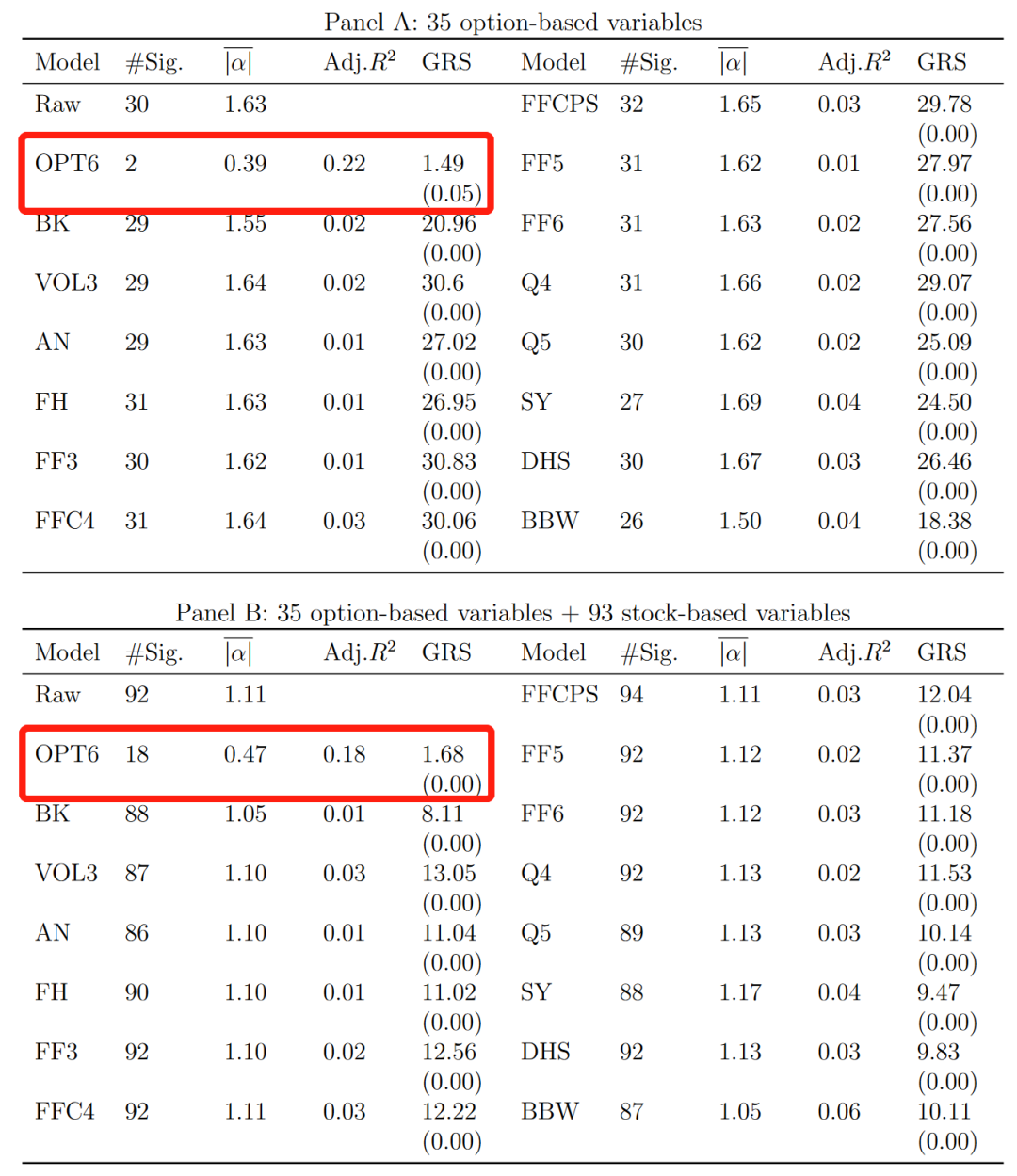
表 2：解释期权异象：不同因子模型的比较. 数据来源：Bali et al. (2022).
4. 期权中的因子动量
基本理解了期权因子和因子模型后，接下来进一步简要看一下期权市场中的因子动量。股票的因子动量在近年来已得到了广泛的研究，川总公众号的推文因子动量和动量因子便对发表于顶刊 JF 的相关研究 Ehsani and Linnainmaa (2022) 做了精彩的梳理和介绍。该文的核心论点是“绝大多数因子的收益率存在自相关性”，且“和个股收益率协方差矩阵更相关的因子，自相关性更强”（根据无套利条件可得）。据此可进一步推论：因子较为重要的主成分中，因子动量更为显著，重要主成分中的因子动量可以解释其他主成分中的因子动量；且因子动量可以解释个股动量（乃至个股残差动量）。
那对于期权而言，是否也有类似的现象呢？
Käfer, Moerke and Wiest (2023)（KMW (2023)）旨在回答上述问题。为此，KMW (2023) 基于期权和股票特征，构建了 56 个期权因子，进而考察期权市场中的截面因子动量和时序因子动量。
他们发现期权因子收益也存在显著的自相关性，且基于不同回望期的因子动量策略都可以获得显著的收益。表 3 报告了具体结果。Panel A 报告了基于过去 1—60 月的因子收益的时序因子动量的年化收益和 Sharpe ratio。结果显示，虽然基于不同回望期的策略表明有所差异，但所有策略的超额收益都非常显著，基于过去 12 个月因子收益的策略的 Sharpe ratio 甚至能超过 3。Panel B 则报告了截面因子动量的表现，总体来看也是非常显著的。进一步的分析还表明，上述因子动量的收益不能被 56 个因子的平均收益（类似于因子市场组合）所解释，也不能被已有研究发现的因子模型所解释。
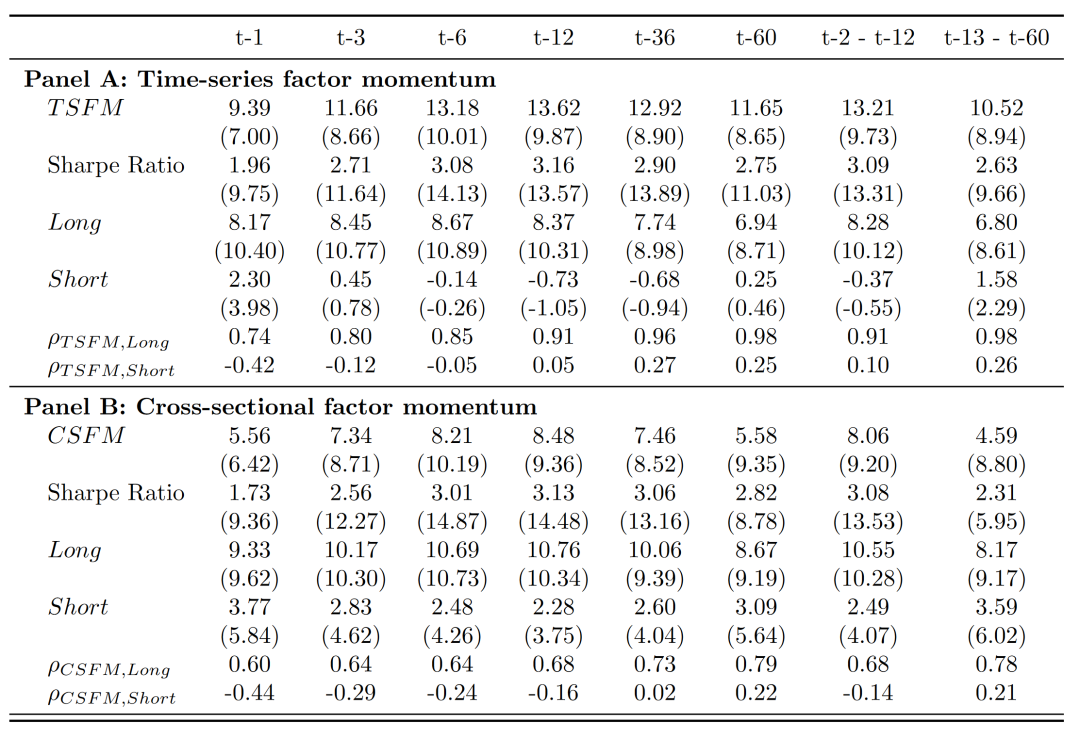
表 3：期权因子动量表现. 数据来源：KMW (2023).
进一步，为理解时序因子动量和截面因子动量的差异，KMW (2023) 进一步比较了二者相互的解释力。结果表明，在大多数回望期下，时序因子动量可以解释截面因子动量，但反之则不然。这一结果对于基于过去 1 月的因子收益构建的因子动量策略尤为显著：1 月期截面因子动量相对于 1 月期时序因子动量的 alpha 为 0.05%(t=0.17)，原因是短期因子动量几乎完全由因子的自相关性所驱动。
此外，Leippold and Yang (2021) 表明股票中的时序因子动量很大程度上来自于买入并持有有正的历史收益的因子。KMW (2023) 对期权因子动量进行了类似的分解，并得到了相似的发现。
KMW (2023) 还参照 Ehsani and Linnainmaa (2022) 考察了因子的不同主成分中的因子动量的相对表现，并得到了不完全相同的发现（见表 4）：
一方面，与 Ehsani and Linnainmaa (2022) 一致，KMW (2023) 发现，在前十大主成分、也即最重要的主成分中，因子动量显著更强；
但另一方面，KMW (2023) 发现，与 Ehsani and Linnainmaa (2022) 关于股票因子动量的发现不同，在那些相对不重要的主成分中，期权因子动量仍然显著，尤其是在控制了基于前十大主成分所构建的因子动量之后（Panel B）。KMW (2023) 为此给出了两个可能的解释：首先，期权市场中，预期收益对因子动量也有显著的影响，而不仅仅是自相关在起作用，这意味着不那么重要的主成分也会有显著的影响；其次，最优期权组合的 Sharpe ratio 平方显著高于最优股票组合，这意味着不那么重要的主成分也可能贡献更多的可预测性。
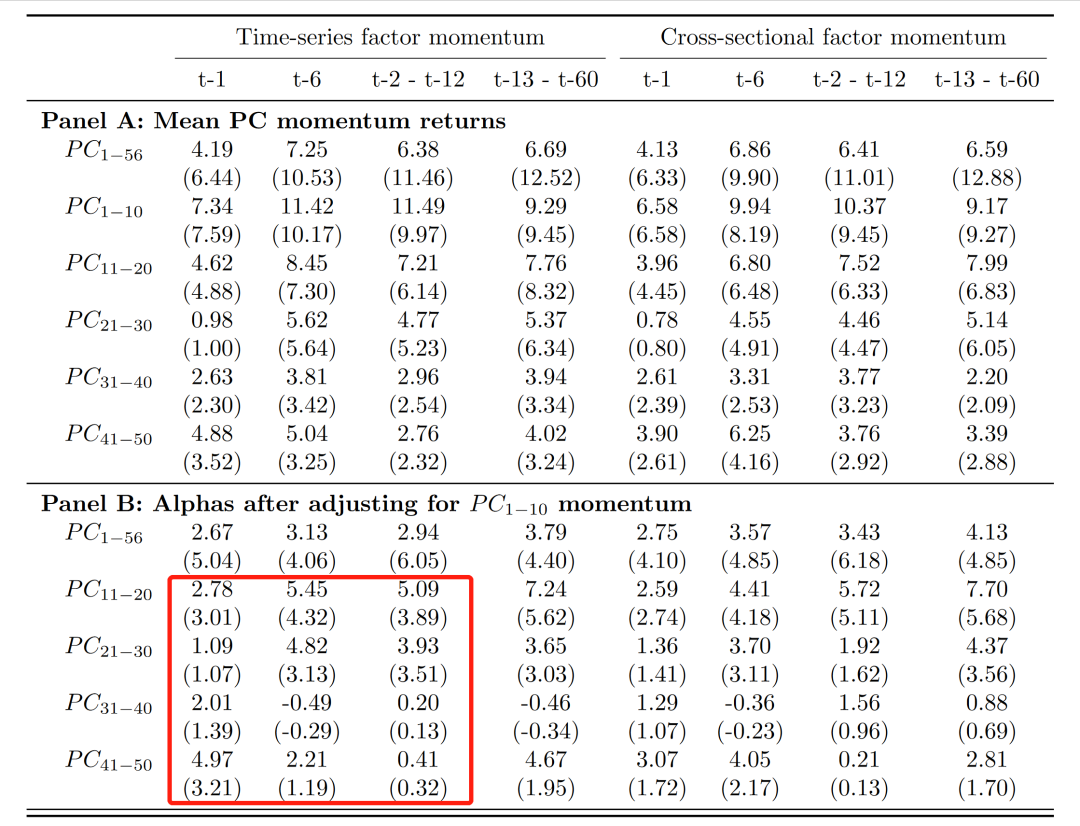
表 4：不同主成分中的因子动量. 数据来源：KMW (2023).
5. 结语
本文对期权因子、因子模型及因子动量的一些代表性研究和新近研究做了简要的梳理，以期通过本文这一简短的篇幅帮您快速建立对期权因子研究的一个概览。但要再次强调的是，本文只涉及了一小部分代表性文献，且对于这些文献也仅梳理了其核心发现。关于股票期权因子的研究，还有为数不少的已有研究，本文所介绍的文章中也有很多未展开讨论的有意思的细节。您如果对期权因子研究这一领域感兴趣，还是应更为仔细地阅读本文所介绍的文章的原文，及其所引用的已有研究。
但无论如何，随着我国期权市场的快速发展，对期权定价、交易更为深入的理解，无论对投资实践，还是对实证资产定价的学术研究而言，都是值得关注的领域。希望这篇小文章可以让您跟园长一样，对这个新领域感到兴奋，一起更仔细、深入地去进行学习和研究。
全文完。祝您阅读愉快！
