Transformer在量化投资中的应用

量化投资与机器学习微信公众号，是业内垂直于量化投资、对冲基金、Fintech、人工智能、大数据等领域的主流自媒体。公众号拥有来自公募、私募、券商、期货、银行、保险、高校等行业30W+关注者，曾荣获AMMA优秀品牌力、优秀洞察力大奖，连续4年被腾讯云+社区评选为“年度最佳作者”。

标题：Time Series Forecasting with Transformer Models and Application to Asset Management

作者：Edmond LEZMI、Jiali XU

开篇

深度学习的发展为我们创建下一代时间序列预测模型提供了强大的工具。深度人工神经网络，作为一种完全以数据驱动的方式学习时间动态的方法，特别适合寻找输入和输出之间复杂的非线性关系的挑战。最初，循环神经网络及其扩展的LSTM网络被设计用于处理时间序列中的顺序信息。然后，卷积神经网络被用于预测时间序列，因为它们在图像分析任务中的成功。

Transformer模型随后于2017年由谷歌发布(Vaswani et al.， 2017)，其设计目的是使用注意力机制处理序列数据，以解决自然语言处理（如机器翻译）中的序列学习问题。本质上，Transformer模型使我们能够将一个域的输入序列转换为另一个域的输出序列。例如，我们可以使用Transformer模型训练机器人将英语句子翻译成法语。打个比方，如果我们把时间序列的一个片段看作是一种语言的句子，下面的片段看作是另一种语言的句子，那么这个多步时间序列预测问题也是一个序列学习问题。因此，Transformer模型也可用于解决时间序列分析中的预测问题。如Wen et al.(2022)所述，Transformer模型的许多变种已成功应用于时间序列预测任务，如Li et al.(2019)和Zhou et al.(2021)。随着Transformer模型架构的提出，深度学习在时间序列预测的应用也越来越广泛。针对时间序列预测存在的难点，越来越多的Transformer的架构被提出，例如Temporal fusion transformers，Informer，Autoformer及Crossformer等。

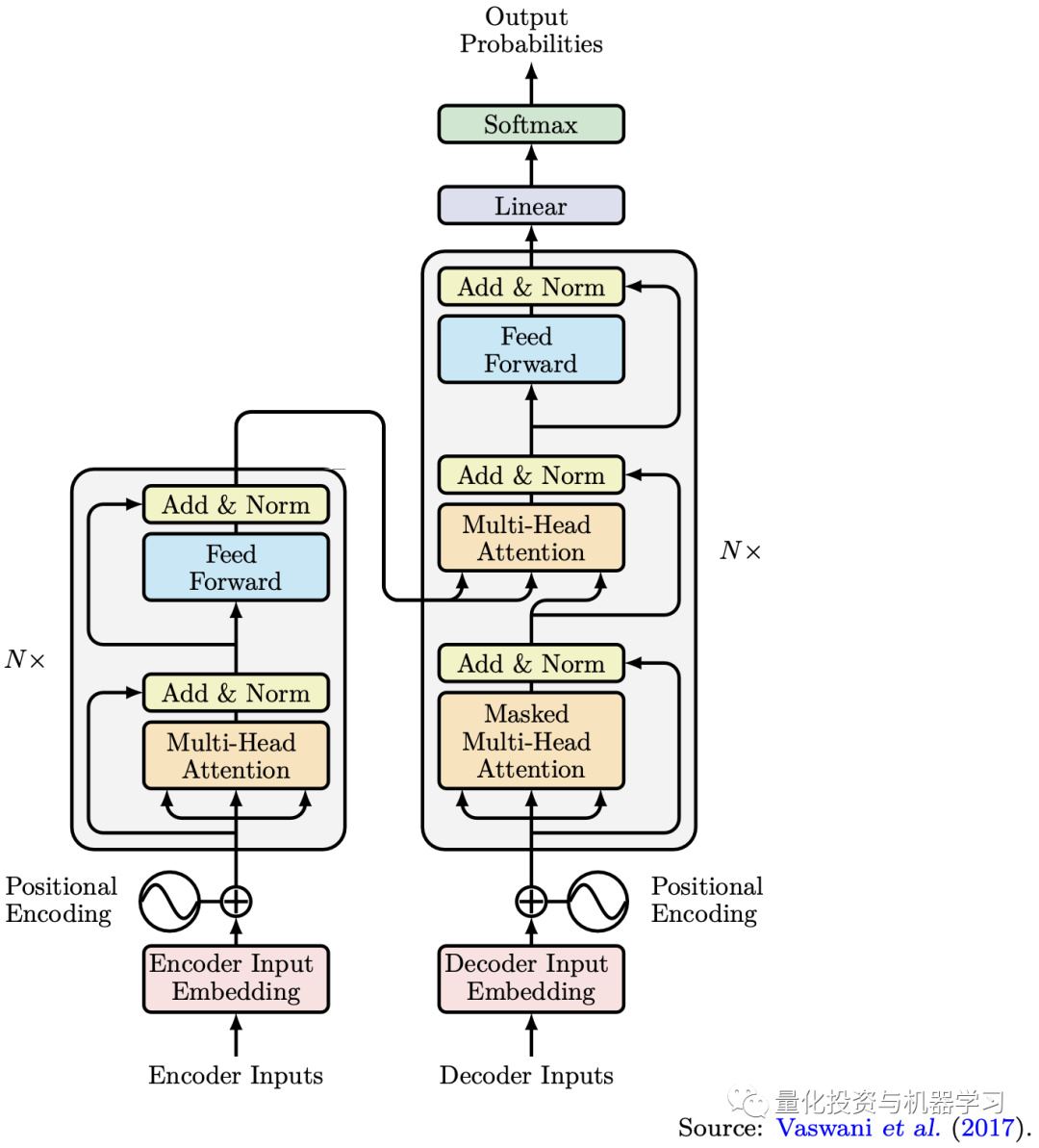
Transformer模型使用了seq2seq架构，其灵活性允许我们处理更复杂的序列学习问题。利用注意力机制，我们可以捕捉序列中元素之间的长期依赖关系，特别是利用多头注意力会从不同方面捕捉序列中的信息。此外，除了我们应用于编码器和解码器的自注意机制外，我们还使用另一种注意机制来捕捉编码器和解码器之间的相关性。由于自关注机制不按时间顺序分析它们的输入，Transformer模型不太可能受到消失或爆炸梯度问题的影响。Transformer模型的另一个优点是它们的并行化。由于采用了多头注意机制，Transformer模型中的每个头都可以捕获输入中的元素与不同标准上所有其他元素的关系。而RNN模型需要将数据按时间顺序逐一输入，这使得其无法并行化。

通过理解Transformer模型的注意力机制原理和seq2seq架构，我们可以将这些先进的机器学习技术应用于时间序列预测，特别是多时段多元时间序列预测，如下图所示。在这类任务中，我们不仅需要学习时间序列中的时间关系来为动态系统的演化建模，还需要学习多元数据中的空间关系来理解它们是如何相互影响的。在金融领域，时间序列预测是一项常见的任务。

Transformer在金融时序预测中，一般有两类应用场景：

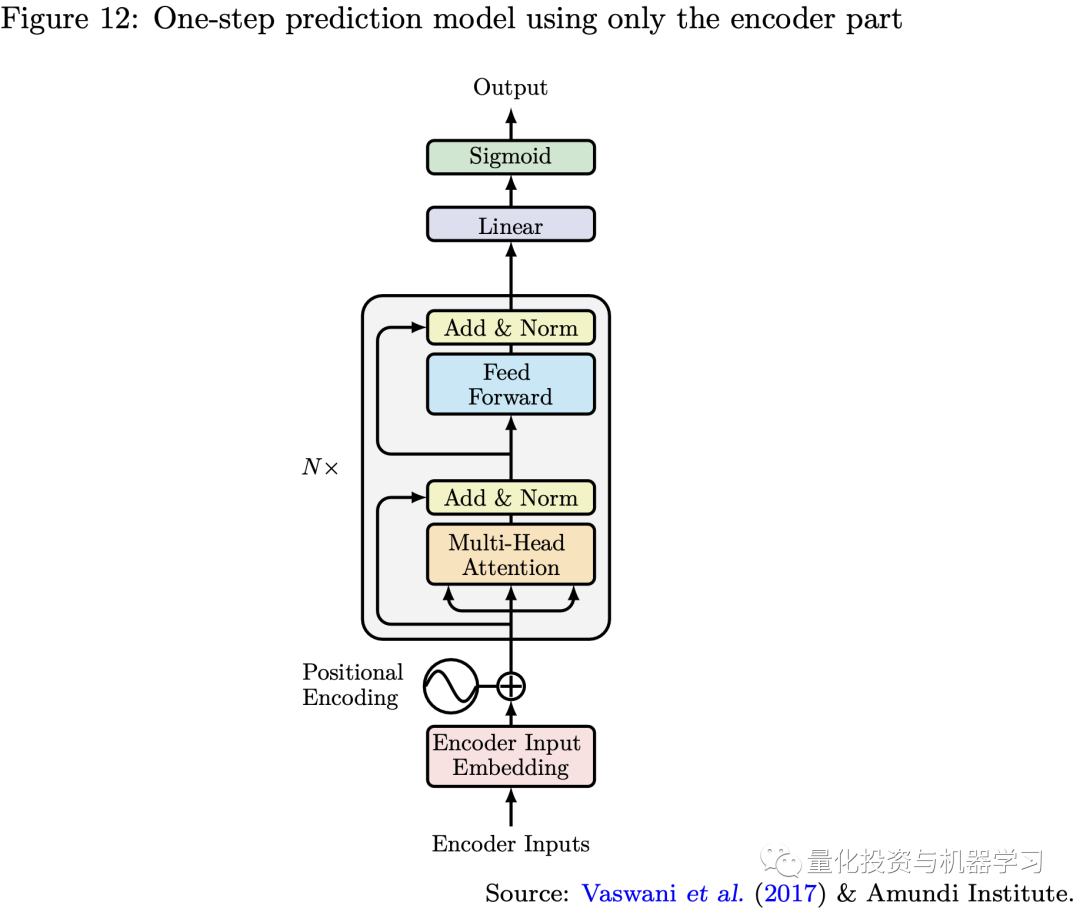
只使用Encoder做单步预测

如下所示，如果我们只使用Transformer模型的编码器部分，并将编码器输出直接连接到最后一层，则该模型类似于传统的RNN的多对一预测，但采用了自我注意机制。因此，我们可以在一步预测问题中使用该模型，就像我们经常使用RNN或LSTM等递归模型一样，这些递归模型可以完全被编码器取代，因为它允许更灵活的并行化，更有效的长期记忆，以及更少的消失或爆炸梯度问题。我们还可以通过修改模型最后一层的激活函数来处理不同的问题，如分类问题，处理回归问题。

使用全模型（Encoder和Decoder）做多步预测

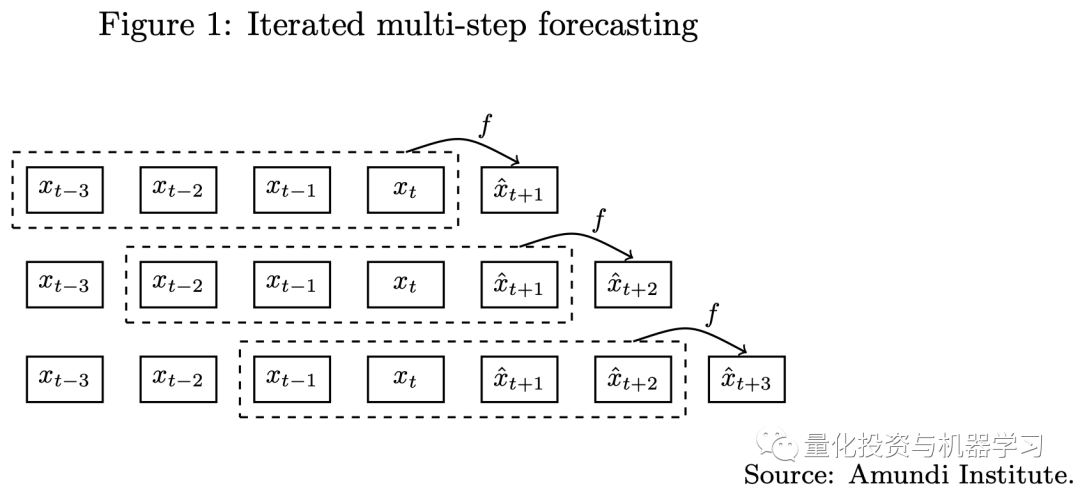
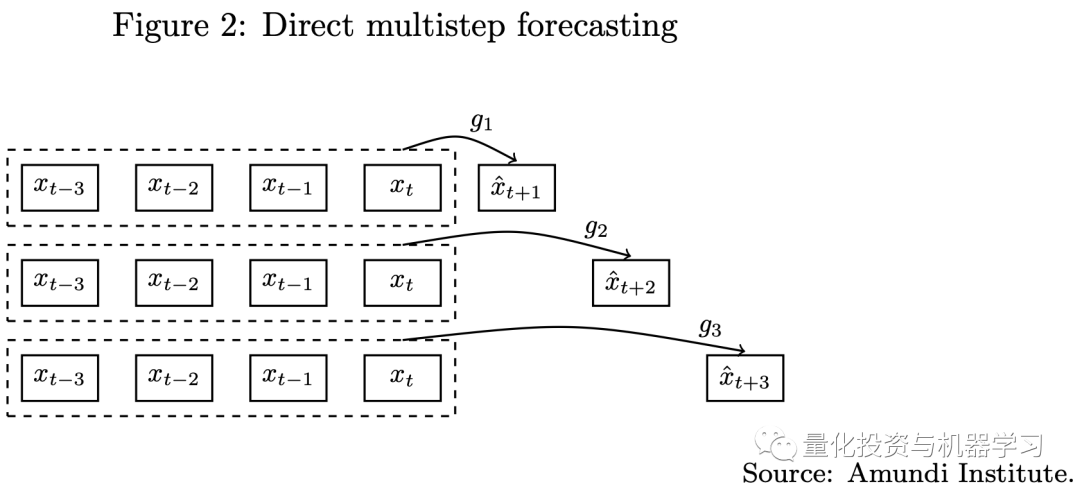
传统的多步预测有两种方式，包括迭代法和直接预测法（如下图所示），无论是使用迭代法还是直接法，一步预测模型都难以应用于多步预测任务。由于Transformer模型中的seq2seq架构，我们可以使用这些模型来处理多步预测问题。

金融时序预测存在的问题

在投资领域，投资组合构建中最困难也是最重要的任务之一就是对未来收益的预测。我们还认为，机器学习模型可能会给量化投资带来一些计算优势，例如捕捉非线性关系和时间依赖性的能力。例如，Cherief等人(2022年)使用基于树的机器学习算法来捕获非线性，并检测欧元和美元信贷空间中风险因素之间的相互影响。

然而，我们认为，机器学习模型的成功应用需要满足许多条件：数据必须干净，数据量也必须足够，数据中呈现的模式必须持久，模型的复杂性必须适当，训练的质量也必须非常好。

在实践中，由于金融时间序列数据与文本或图像等其他领域的数据存在差异，我们往往无法满足上述所有条件。主要的问题有：

低信噪比

与图像处理或自然语言处理等传统机器学习技术用例不同，金融数据中的信噪比非常低。换句话说，数据中有太多的噪音，因此系统不够可预测。值得指出的是，如果我们考虑一个分类或回归问题，噪声不仅存在于特征中，也存在于标签中。例如，我们可以将资产的回报看作是预期回报和噪声的总和。我们可以很容易地从市场数据中观察到已实现的回报，但要知道真正的预期回报是什么是非常困难的，特别是在噪声非常强的情况下。

市场是不断发展的

这就是为什么“体制转换（Regime Shift）”一词被用来描述金融体系中几个组成部分之间的相互联系的变化。作为一个经典的例子，我们用扩张或衰退来描述经济周期的不同机制，用牛市或熊市来描述金融市场周期。为了训练一个鲁棒的机器学习模型，除了确保训练和验证数据集具有类似的分布外，我们还必须确保未来的数据也遵循相同的分布。对于大多数金融数据，这两点很难实现。因此，如果我们希望有一个可以适应当前制度的机器学习模型，用于训练模型的输入不应该包括太旧的数据。

金融行业的数据量较少

主要问题是，所有的金融数据都是随机和非平稳的，这使得很难通过跟踪金融市场的时间动态的实验产生新的数据。此外，规模限制不仅来自特征，而且往往来自标签，因为我们更希望能够直接预测有有限观察的金融资产的回报。例如，如果我们有一项金融资产的20年日回报率，那么也只有大约5000个数据点，分布在不同的市场Regime中。对于一些极端事件，发生的次数要低得多，如金融危机、新冠肺炎等。这个数量级的数据相对于其参数数量来说不足以训练一个深度学习模型，特别是在多元的情况下。因此，除了上一段介绍的原因外，用于训练模型的数据集的容量经常受到限制。

怎么权衡模型的复杂性

当我们在量化投资中使用机器学习技术时，特别是做资产收益的分类或回归时，我们往往会将所有特征输入一个复杂的深度学习模型，希望捕捉金融数据中的非线性关系和复杂结构。基于我们之前提到的机器学习在金融应用中的三个问题，我们很容易犯两个错误:

1、由于金融领域的数据质量和数量不如许多其他使用机器学习技术的领域，模型的准确性将不够高，以确定模型是否良好和稳健。特别是，我们用于机器学习的标签，例如资产回报的正负符号，非常不稳定、嘈杂，有时是错误的。因此，使用这些低质量的标签和复杂的模型将导致模型一无所获或过拟合。

2、根据我们的经验，我们发现，在没有足够数据进行训练的情况下，使用复杂的深度学习模型会有更强调某些特征的趋势，这意味着模型往往会过度拟合。在这种情况下，我们将面临失去多元化的问题，这是量化投资中最重要的一点之一。

因此，在我们无法显著提高模型精度的情况下，使用具有非常多特征的复杂深度学习模型的样本外性能往往低于传统的基于规则的模型，因为在试图捕获数据中更复杂的关系时，我们同样失去了利用多样化的机会。因此，我们认为，我们应该在模型复杂性和多样化之间选择一个平衡。受集成学习中弱学习器概念的启发，我们在实践中倾向于训练许多结构简单、使用较少特征的弱模型。然后，我们通过加权所有模型的预测来构建一个强大的模型，而不仅仅是训练一个复杂的机器学习模型。此外，我们选择了不同类型的弱模型，因为我们希望它们从不同方面获得有用的信息。在训练各类弱模型时，我们应尽可能少地使用参数/超参数以避免过拟合，同时使用不同的超参数集以获得更稳健的结果。使用较少的特征来训练模型的另一个优势是，使用相对较少的数据，即使使用神经网络结构，也可以很好地训练模型。

使用来自金融领域的数据构建非常复杂的机器学习模型是极其困难的，因为用于训练模型的数据包含许多缺陷。因此，我们的目标是牺牲模型的复杂性，以获得更好的校准和预测质量，这意味着模型与财务数据拟合的难度更小，样本外误差更小。我们认为，这是一个非常适合机器学习在量化投资中的应用的解决方案，在量化投资中，数据的质量和数量相对低于行业，我们无法找到一个明确的规律来全面描述市场中的行动。模型复杂性的牺牲将通过量化投资的多样化得到补偿。因此，当我们希望应用传统的机器学习模型或深度学习模型来预测资产的未来回报时，我们更倾向于使用结构简单、特征较少的低复杂度模型，例如Transformer模型，其编码器和解码器部分的深度较小，使用两到三个特征作为输入。在这种情况下，人们仍然使用深度学习模型，是为了利用它们处理时间序列和捕获数据中的长期记忆的能力，而不是利用它们的能力来拟合具有非常深结构的复杂非线性关系。

这种方法，在保持多样化原则的基础上，与Vapinik-Chervonenkis理论是一致的，该理论试图为学习过程提供统计解释。根据Vapnik(2000)，在训练机器学习模型时，我们需要在模型复杂性、校准质量和预测质量之间找到平衡。在深度学习的背景下，模型复杂度是指模型中使用的参数数量，如神经网络的层数、每层的节点数等。更多的参数意味着更复杂的模型，可以学习到数据中更复杂的关系，但在训练过程中需要更多的数据进行模型校准。校准质量是根据训练误差和模型的复杂性来衡量的，为了提高校准质量，数据必须相互匹配。例如，过于简单的模型无法捕获数据中的所有信息，线性模型无法找到训练数据集中的非线性关系，而过于复杂的模型则需要大量高质量的数据进行训练，这通常是不可能的。预测质量与模型的样本外误差有关，复杂的模型往往容易发生过拟合，从而导致较大的样本外误差。

Transfomer在量化投资中的案例

案例1：趋势跟踪策略（单步预测）

我们首先看一个单步预测的案例。在趋势跟踪策略的情况下，我们将使用Transformer模型的编码器部分，使用资产的短期、中期和长期趋势来预测资产下周回报的迹象。在我们的例子中，我们没有将所有这些特征放在一起来训练一个复杂的模型。我们借鉴了集成学习中弱学习器的思想，我们将训练许多模型，每个模型都很简单，只使用一两个特征。最后，我们将这些弱学习器聚集起来，成为一个强学习器。

我们采用logistic回归、支持向量机和带有注意力机制的编码器等不同模型，对各资产下周的超额收益进行分类预测（是一个分类模型）。对于每个模型，我们用一两个特征训练弱学习器，并将所有弱学习器的结果进行聚合，以构建一个强学习器。为避免选择偏差，我们用5个经典回溯窗口(1个月、2个月、3个月、6个月、12个月)计算资产的短期、中期、长期的收益率作为模型的特征集。

该回测的目的是说明在将机器学习模型应用于量化投资时，模型复杂性和多样化之间权衡的重要性，并测试机器学习模型是否可以在数据中捕获更多的信息。我们使用不同的模型从数据的不同方面获取信息：

1、基准策略相当于一个线性分类器，只训练一个特征，例如，12个月的动量，阈值设置为0.9。

2、逻辑回归也建立一个线性分类器训练上只有一个特征，但阈值是从数据中学习。

3、为了使用支持向量机中使用的RBF核（径向基函数核）捕捉数据中的非线性关系，我们一次使用两个特征训练一个模型，比如1个月和12个月的动量。当我们有5个特征时，我们必须训练10个模型。

4、我们还对编码器进行了多头注意机制的训练，以捕获时间序列维度的信息。用于校准模型的特征仍然是使用5个不同的回顾窗口的趋势，但这些特征作为时间序列输入模型。我们将应用与之前相同的想法，每个模型也使用两个特征进行训练。

对于每个模型，如果我们需要为模型选择超参数，我们将选择一组超参数而不是一个，并对使用不同超参数的所有模型的预测结果进行平均。对于我们采用多头注意机制的编码器，我们采用了2个编码器块的简单结构，由于我们的设计是只使用少量特征作为输入来训练模型，所以这个线性层不需要有太多的节点。

回溯中，我们使用每周再平衡，并将期货交易成本设置为2bps。我们每3个月根据过去3年的观察数据重新校准机器学习模型。由于模型训练过程中的随机效应，我们在每个重校准日期在同一训练数据集上训练多个模型，然后对所有模型的预测结果进行平均。以下是不同类型模型的回测结果：

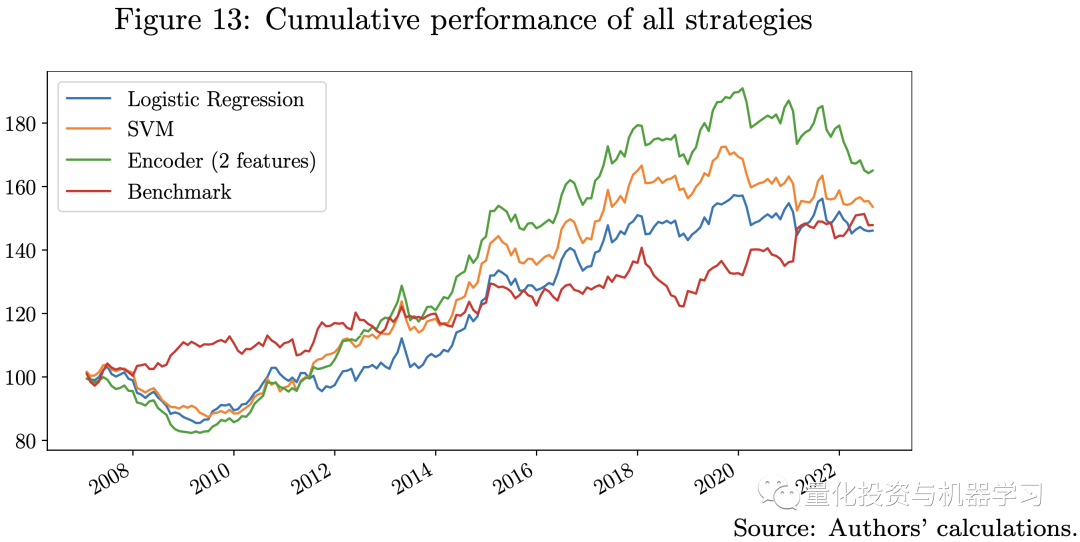
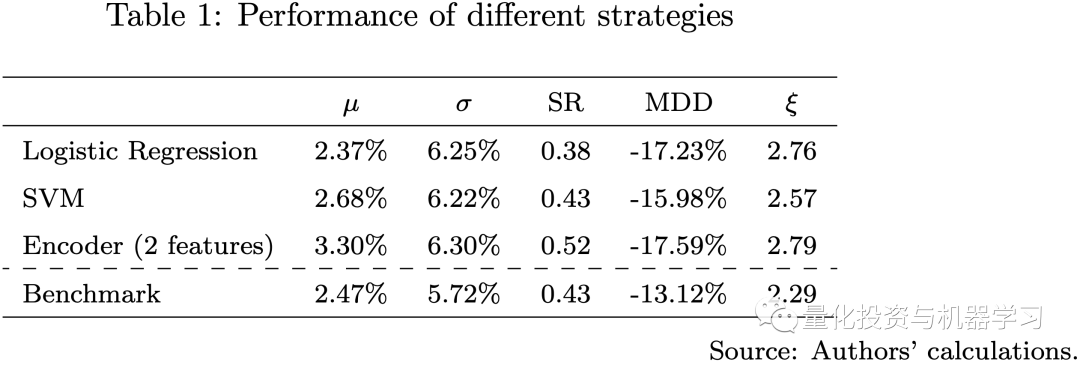
从上图中，我们注意到所有使用机器学习模型的策略相对于基准策略的表现有很大不同。Logistic回归和SVM模型的Sharpe比率与基准策略相当，具有多头注意力机制的编码器优于所有其他模型。所有策略都有相同的波动水平和最大回撤。我们的三个机器学习模型具有不同级别的模型复杂性，并使用不同数量的特征进行训练。在这方面，模型越复杂，就越有可能捕获数据中的有用信息。我们在回测中观察到2020年之后，所有机器学习模型都在挣扎，在这个时期，Covid-19、高通胀、加息、股票和债券之间的高度相关性以及俄罗斯-乌克兰战争使金融市场比以往任何时候都不同。

由于样本外误差较大，模型越复杂，我们在这一时期的表现就越差。这就是为什么编码器模型在2021年后迅速下降的原因。在这种情况下，可行的选择是增加模型重新校准的频率，并在训练过程中使用更近期的数据，以快速适应实际的市场情况。回测结果表明，使用机器学习模型可以在数据中捕获更多有用的信息来预测未来的收益，因此我们可以尝试通过在模型中添加一些宏观因素来改进策略。

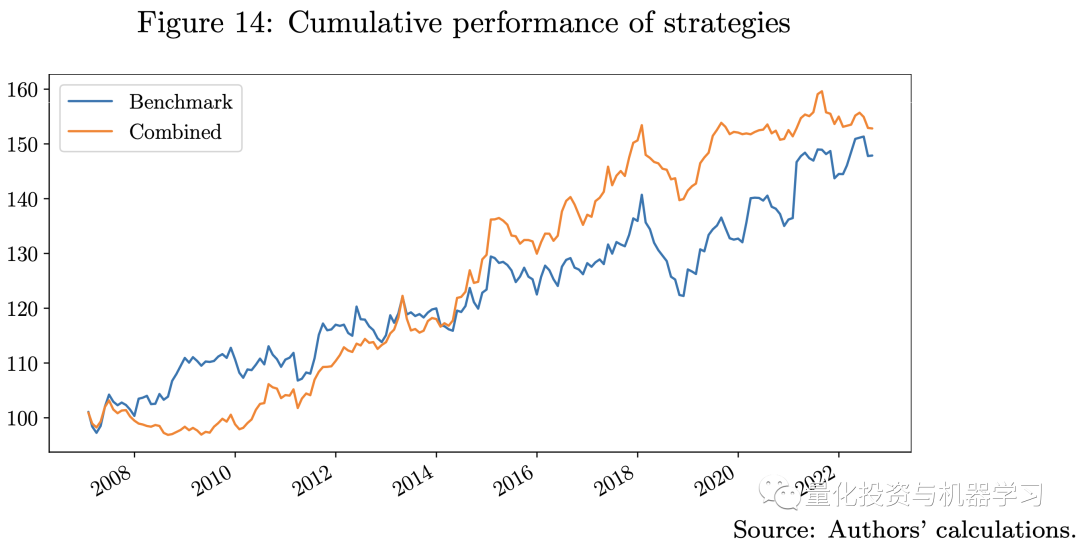
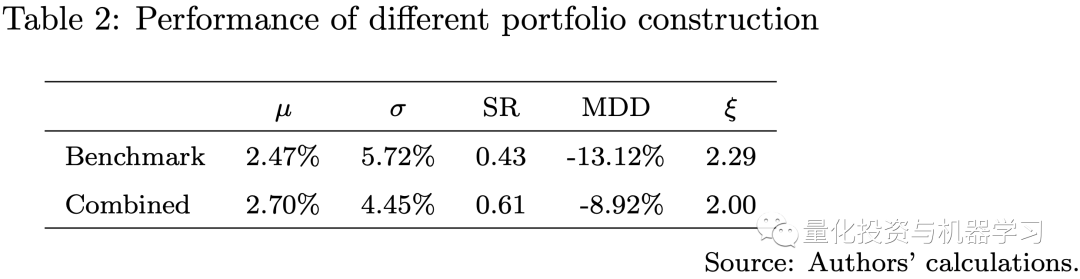
在下图中，我们展示了基准策略和集合策略的比较，集合策略结合了3种机器学习策略和基准策略，采用了风险平价方法。集合策略的表现优于基准策略，夏普比率更高，最大跌幅更低。这一结果表明，机器学习模型可能在量化投资方面提供一些计算优势。特别是确认了我们策略设计的关键思想，即训练许多弱机器学习模型来构建强学习者，以确保模型复杂性和保持多样化之间的平衡。

案例2：组合优化（多步预测）

对于多期投资组合优化问题，我们将使用全Transformer模型对波动率时间序列进行多期预测，并将这些预测作为平均方差优化方法和风险预算方法等投资组合配置方法的输入。我们将比较单期最优投资组合、基于历史估计的多期最优投资组合和基于Transformer预测的多期最优投资组合之间的差异。

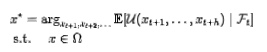
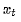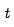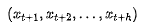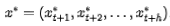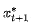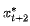对于多期的组合优化，目标是最大化未来h期的效用。如上述等式中，是期的持仓权重向量,是未来h 期的持仓权重。是效用函数。假设以上优化求解的问题的解为 。但实际上在  时刻，我们最看重，因为会在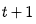根据最新的信息进行更新。

然而，多期投资组合优化模型在实践中应用较少。一个原因是，准确估计多个时期甚至一个时期的回报/风险可能是相当具有挑战性的。在MVO模型的框架下，我们需要估计投资组合中资产的预期收益向量µ和方差-协方差（VCV）矩阵Σ。此外，VCV矩阵可以分为波动率向量和协方差矩阵。经验上，预期收益向量被认为是MVO模型中这三种输入中最难估计的，而协方差矩阵通常被认为比预期收益和波动率更稳定。因此，波动率预测是定量研究中的一个重要问题。

波动性作为衡量市场风险的标准，被广泛应用于整个金融行业的各种应用中。特别地，所有传统的投资组合构建方法都将资产的波动性作为模型的输入，无论是均值-方差优化方法还是风险平价/风险预算方法。波动率预测问题的核心可以看作是一个时间序列预测问题。在我们的研究中，我们将利用Transformer模型中的注意力机制和seq2seq架构来解决这些问题。

在实验中，我们并没有直接使用Transformer模型预测整个VCV矩阵，而是分别预测各资产的波动率，然后使用1年历史资产收益率和预测的波动率构建协方差矩阵构建VCV矩阵。其原因是Transformer模型不能保证返回正的半定矩阵，而多元时间序列预测需要模型中更复杂的结构和更多的数据来训练模型。因此，通常很难获得好的结果。

策略的调仓期是月度调仓，但我们使用周度的数据进行波动率预测，也就是需要一次预测未来四个周的波动率（如下图所示），这正是一个多步预测模型。

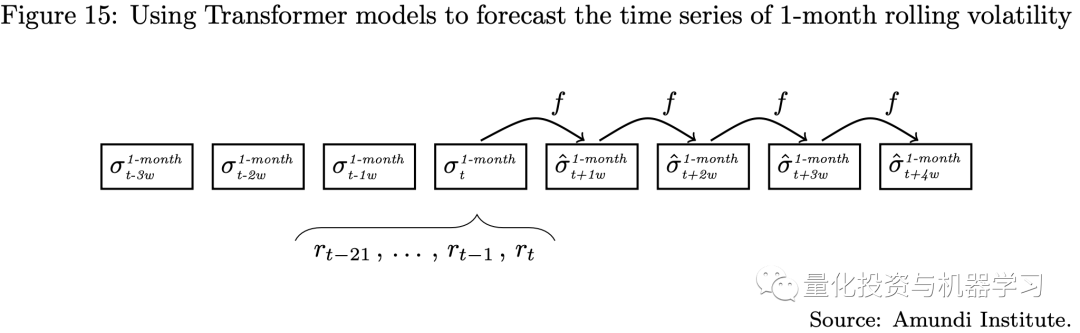
在我们的实验中，我们考虑了三种不同的投资组合配置方法：

1、基于MVO的每月调仓

2、基于风险平价每月调仓

3、基于多期MVO的每周调仓

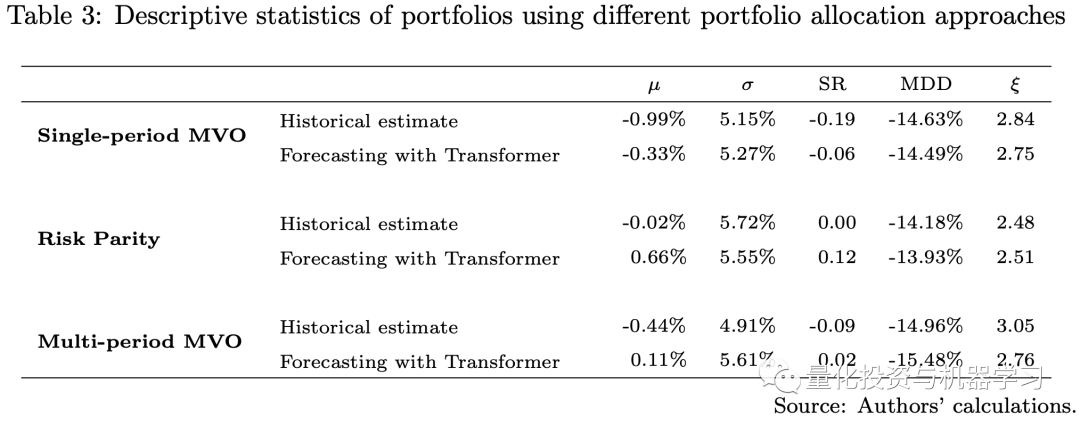
下图展示了回测结果。鉴于我们的测试期恰逢Covid-19和俄乌战争造成的经济挑战期，而所有三个投资组合都是只做多的投资组合，它们都在2022年经历了重大损失。然而，使用Transformer模型的预测作为输入的投资组合的业绩优于使用历史估计的投资组合。使用Transformer模型的投资组合具有更高的Sharpe比率。我们的每周再平衡多期MVO投资组合表现优于单期MVO投资组合。由于风险平价投资组合仅使用VCV矩阵的估计作为输入，故我们不包括模型中对回报的估计误差，这些误差通常较VCV矩阵更难估计。因此，在这一经济充满挑战的时期，风险平价投资组合的表现优于MVO投资组合。

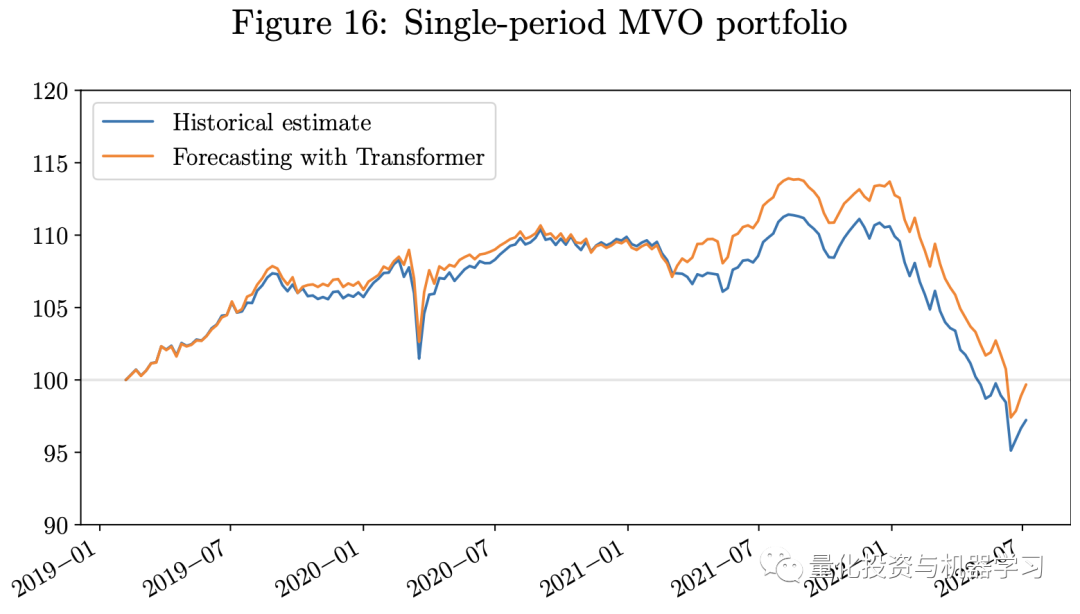
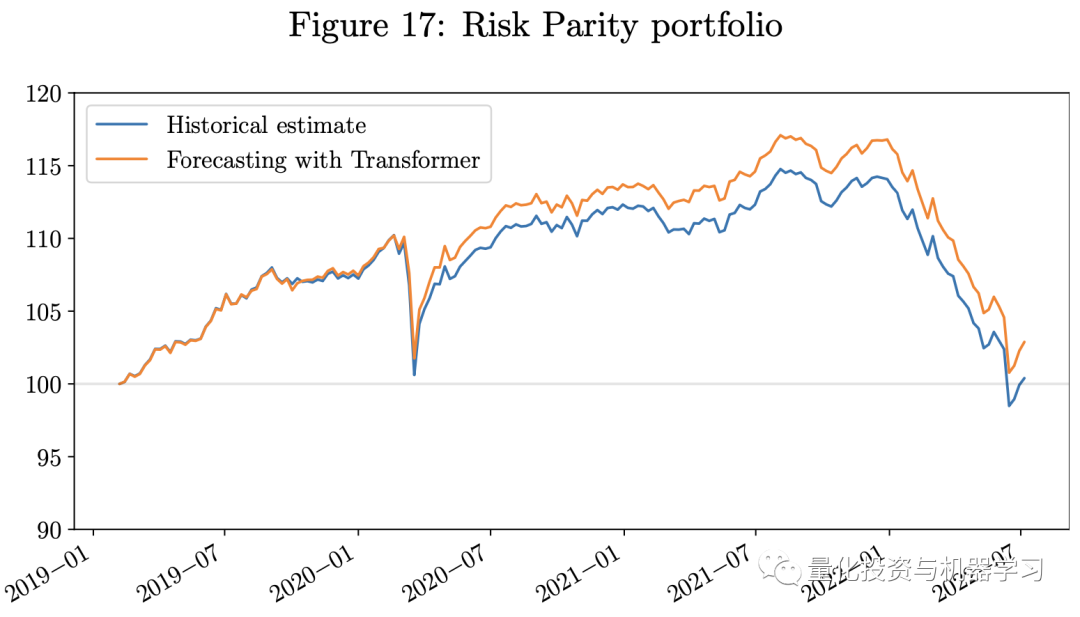
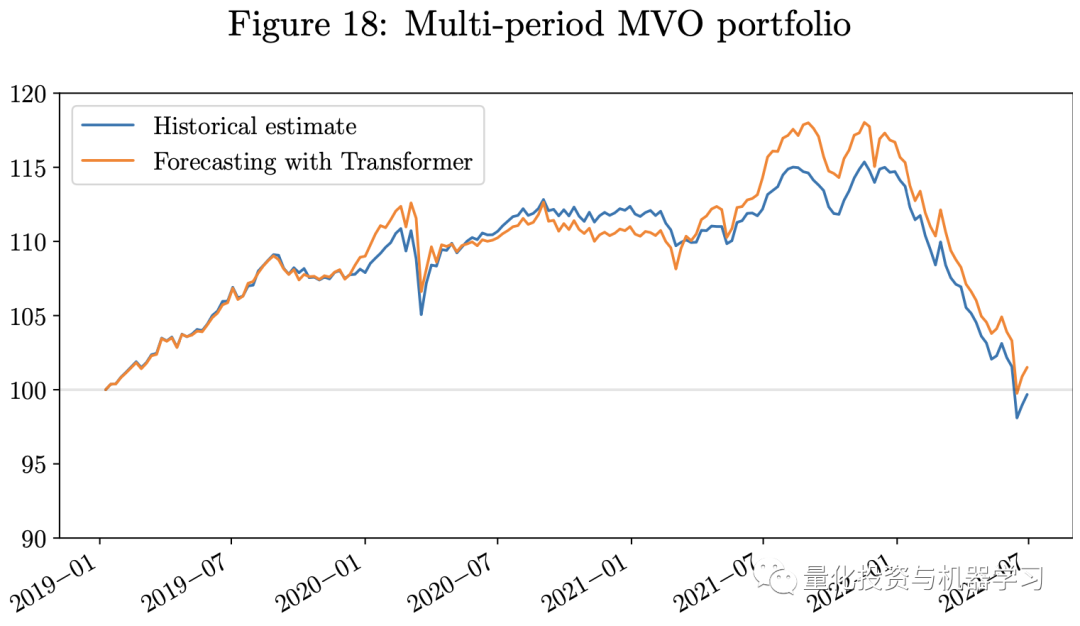
最后

正如我们在本文中描述的那样，在金融中应用机器学习技术时的主要困难是金融数据中的信噪比往往较弱。因此，下一阶段的研究重点是金融数据的去噪和标注，这是机器学习技术在金融领域成功应用的关键。特征工程对于时间序列预测也很重要，我们可以通过模式分解技术将时间序列分解为趋势、季节性和噪声成分。将这些方法与深度学习模型结合使用是一个有趣的研究课题。其次，正如我们在关于图神经网络的工作论文(Pacreau et al.， 2021)中描述的那样，注意机制也被用于图注意层(GAT)中，以捕获数据维度之间的底层关系。因此，尝试将Transformer模型和图神经网络(GNNs)相结合，来管理多元的、时空的时间序列数据，如流量预测，是很有效的。一些研究人员声称，这种模型组合可以提高性能，并在时空时间序列预测中更好地理解数据的因果关系，如Cai et al.(2020)和Xu et al.(2020)。

在金融领域，多家公司之间的关联关系或供应链关系可以看作是一种空间关系。因此，将Transformer和GNN结合起来，对时间序列的动态和维度之间的依赖性进行建模是我们未来研究的一个重要途径。这将为一个新的研究领域打开大门，以捕捉财务数据中更复杂的关系，并改进量化投资策略。

参考文献

Cai, L., Janowicz, K., Mai, G., Yan, B. and Zhu, R. (2020), Traffic Transformer: Capturing the Continuity and Periodicity of Time Series for Traffic Forecasting, Transactions in GIS, 24(3), pp. 736-755.

Vapnik, V. (2000), The Structure of Statistical Learning Theory, Second edition, Springer.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, L. and Polosukhin, I. (2017), Attention is all you need, NIPS’17: Proceedings of the 31st International Conference on Neural Information Processing Systems.

Pacreau, G., Lezmi, E. and Xu, J. (2021), Graph Neural Networks for Asset Management, ResearchGate, https://www.researchgate.net/publication/356634779.

本文来自微信公众号“量化投资与机器学习”，文章版权归原作者所有，内容仅供参考并不构成任何投资及应用建议。