资产定价中的实证挑战 (II)

作者：川总写量化

题图：川总写量化 微信公众号

0

如前文《资产定价中的实证挑战 (I)》所述，现如今，实证资产定价研究范式从计量经济学转向了机器学习；而这背后的驱动因素来自（至少）两方面的实证挑战：（1）协变量的高维数；（2）公司特征和收益率之间的复杂关系。

作为第二篇，本文聚焦公司特征和收益率之间的复杂关系。

1

资产收益率代表了投资者关于资产未来现金流的预期；这一预期建立在每个投资者各自掌握的信息集之上。大数据时代协变量的激增让信息集不断扩充；协变量和收益率之间的关系也更加扑朔迷离。作为实证研究者，我们无法观测到投资者使用的所有信息，甚至很难在模型中包含其中的哪怕一小部分信息（Cochrane 2005）。

类似地，我们无从知道投资者使用信息的具体方式，因此也就无法在参数统计模型中做出相应的结构性假设（Kelly and Xiu 2023）。我们可以透过模型的高度不确定性来审视协变量和资产收益率之间的未知复杂关系。此外，协变量之间的交互作用是上述复杂关系的重要体现之一。

2 模型不确定性

Giannone et al. (2021) 研究了大数据时代经济学领域常见的六大类预测问题，其中之一就是实证资产定价。该文在线性模型的框架下，通过两个参数控制模型纳入协变量的概率以及协变量的系数被向先验（零）收缩（shrinkage）的程度（此处，将系数向先验收缩是一种正则化手段）。

对于高维协变量，收缩是防止过拟合的有效手段。通过贝叶斯统计，该文得出了上述参数的后验联合分布并以此给出了诸多非常有益的定量统计推断。在他们考虑的资产定价案例中，协变量被纳入概率的后验均值很高（0.6 左右）且分布紧密围绕在均值周围。其次，从联合分布来看，被纳入的概率越高，协变量系数的收缩的程度也越高（从而防止过拟合）。

Kozak et al. (2020) 的实证结果也支持这一观点，即纳入更多的协变量和施加必要强度的正则化对于模型在样本外的表现至关重要。该文使用 50 个协变量构造因子并研究了它们对于资产定价的作用。实证结果表明，只有当上述两点均满足时才能在样本外获得更好的表现。

此外，Giannone et al. (2021) 还考察了每个协变量被纳入模型的概率。对于我们关心的问题，该文使用的 144 个协变量均有一定的概率被纳入模型。结合所有协变量的整体被纳入概率，我们可以得出实证资产定价问题中并没有明显的稀疏性模式。换言之，每个协变量都有一定可能存在于真实的模型之中，即模型有很高的不确定性。

上述结论在 Bryzgalova et al. (2023) 中得到了进一步确认。该文以 51 个因子的超过 2 千万亿种排列组合所构造的模型为分析对象，发现不存在某个最优的模型，而是存在数百种可能的模型设定，给出了几乎相同的资产定价实证结果（即 cross-sectional model space is FLAT）。

此外，Bryzgalova et al. (2023) 指出，最终的资产定价模型可能由 factor selection 和 factor aggregation“双向奔赴”构成，即有一些因子被纳入 SDF 的概率很高（确定性很高），而其他绝大多数因子都有高度的不确定性。这意味着，在公司特征层面，SDF 是非稀疏的，因此仅仅指望使用极少数变量以构造简约的定价模型（FF3、FF5）是不切实际的。

当然，或许你会问，那么 PCA 以及各种 PCA 的延伸（例如 Risk Premium PCA）如何。实证结果（下图）显示，并非所有的 RP-PC 因子都进入最终的模型；且在被纳入的 RP-PC 因子之外，模型中依然有 standalone 公司特征。这意味着，人们依然不完全清楚如何最合理的 aggregate 公司特征；而更有可能的是处于 factor selection 和 factor aggregation 的某种“平衡”之中。

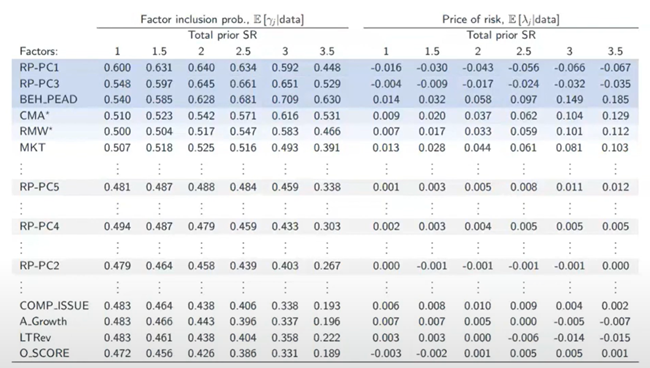
模型的高度不确定性意味着，最佳的预测往往是通过对平均带有不同协变量的模型而获得。这合理地解释了模型平均技术以及更广泛的集成机器学习方法（如提升、装袋和随机森林等）为什么能在实证上取得成功。此外，上述研究对于样本外的启发是，忽视模型不确定性且强加稀疏性假设会造成投资机会的损失。

3 非线性关系

近年来，收益率与协变量之间的非线性关系越来越受到重视（Kirby 2020），特别是在考虑宏观经济因素、交易成本或投资者行为时。

非线性关系可能源于多种原因。首先，资产的收益率会随着时间变化，受到宏观经济周期、货币政策和全球金融危机等因素的影响。其次，交易成本和市场摩擦也可能导致非线性关系。此外，投资者的反应过度以及反应不足也会致使这种现象出现。投资者的异质性和行为也可能导致收益率与协变量之间的非线性关系。不同的投资者可能对信息有不同的反应，或者在不同的时间尺度上做出投资决策，从而影响资产价格和收益率。

从实证角度来说，考虑协变量之间的交互作用而单一协变量的高阶项非是捕捉这种非线性的关键（Bryzgalova et al. forthcoming，Gu et al. 2020，Nagel 2021，Chen et al. 2024）。例如，Gu et al. 2020 通过比较不同模型发现，和仅考虑变量自身高阶项的广义线性模型相比，考虑变量之间相互作用的回归树模型以及神经网络模型能够获得更好的样本外实证结果。

在学术发现中，有关协变量交互作用的一项经典实证研究要数 Stambaugh et al. (2015)。该文从套利风险的角度研究了特质性波动率（idiosyncratic volatility）和收益率的关系。套利风险指的是套利活动常常因为各种原因被阻止。关于套利风险的来源，最常见的便是噪声交易者的行为。套利交易者在价格高估时会卖空股票，但此时噪声交易者可能继续买入，进一步推高价格，甚至最终迫使套利交易者因追加保证金的压力等原因而止损。

鉴于上述假设，该文提出了关于特质性波动率、套利风险以及错误定价三者之间关系的猜想，即特质性波动率越高，套利风险也就越高，因而股票的错误定价就更难以被消除。此外更重要的是：（1）对于被低估的股票而言，其错误定价越严重，则该股票的价格相对其内在价值越低，因此未来的预期收益率越高，这意味着特质波动性和预期收益率正相关；（2）反观被高估的股票来说，其定价错误越严重，则该股票的价格相对其内在价值越高，其未来的预期收益率越低，这意味着特质波动性和预期收益率成反比。从以上论述不难看出，错误定价的程度导致了特质波动性和收益率之间的非线性关系。实证结果证实了他们的猜想。

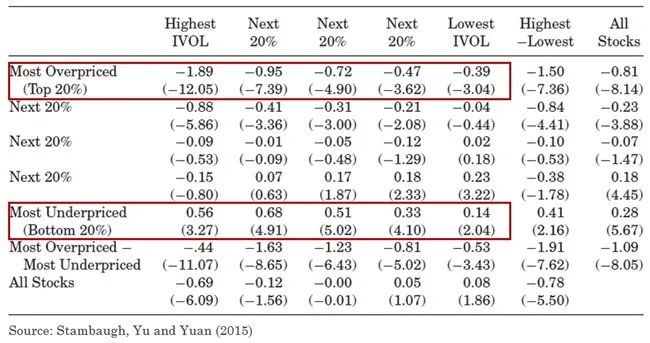
上述结果对于实证研究的另一个启示是，我们可以在控制一个协变量的前提下，研究另一个协变量和收益率之间的关系。这对应着学术界在构造因子是广泛使用的双重排序法（该方法因被 Fama and French 1993 用来构造因子而得以发扬光大）。

与之对应的另一个手段是将协变量的交乘项加入到回归模型之中。然而，哪些变量之间存在交互作用呢？金融学先验在这方面似乎没有给出太多的指引。此外，在协变量的高维数时代，想要穷尽两两变量的双重排序或是交乘项也是不切实际的。在这种困境下，通过数据驱动的方法捕捉隐藏在数据之中的潜在非线性关系或许是可行之道。

以上简要梳理了当下资产定价研究的第二个实证挑战。本文和前文勾勒的两个实证挑战也在很大程度上驱动了实证研究从计量经济学向机器学习转型。

在下一篇，我们将会对比这二者在实证资产定价研究中的异同。

Stay tuned.

参考文献

Bryzgalova, S., J. Huang, and C. Julliard (2023). Bayesian solutions for the factor zoo: We just ran two quadrillion models. Journal of Finance 78(1), 487-557.

Bryzgalova, S., M. Pelger, and J. Zhu (forthcoming). Forest through the trees: Building cross-sections of asset returns. Journal of Finance.

Chen, L., M. Pelger, and J. Zhu (2024). Deep learning in asset pricing. Management Science 70(2), 714-750.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3-56.

Giannone, D., M. Lenza, and G. E. Primiceri (2021). Economic predictions with big data: The illusion of sparsity. Econometrica 89(5), 2409-2437.

Gu, S., B. T. Kelly, and D. Xiu (2020). Empirical asset pricing via machine learning. Review of Financial Studies 33(5), 2223-2273.

Kelly, B. T. and D. Xiu (2023). Financial machine learning. Foundations and Trends® in Finance 13(3-4), 205-363.

Kirby, C. (2020). Firm characteristics, cross-sectional regression estimates, and asset pricing tests. Review of Asset Pricing Studies 10(2), 290-334.

Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271-292.

Nagel, S. (2021). Machine Learning in Asset Pricing. Princeton University Press.

Stambaugh, R. F., J. Yu, and Y. Yuan (2015). Arbitrage asymmetry and the idiosyncratic volatility puzzle. Journal of Finance 70(5), 1903-1948.

免责声明：入市有风险，投资需谨慎。在任何情况下，本文的内容、信息及数据或所表述的意见并不构成对任何人的投资建议。在任何情况下，本文作者及所属机构不对任何人因使用本文的任何内容所引致的任何损失负任何责任。除特别说明外，文中图表均直接或间接来自于相应论文，仅为介绍之用，版权归原作者和期刊所有。