作者:嘟嘟的投研CheatSheet,好投学堂专栏作家
题图:嘟嘟的投研CheatSheet微信公众号
无处不在的组合投资
有些朋友认为,做FOF的门槛很低,就像“鸡蛋不要放在同一个篮子里”那般简单,殊不知,不恰当的组合可能会出现“篮子砸了鸡蛋全碎”的情形。
做好FOF需要两维度的能力:一个是对单一策略的理解,另一个是组合管理的能力。
但组合管理的思维不局限于FOF,单策略开发也蕴含着非常多组合管理的理念。比如量化股票/CTA,当我们挖掘出很多个有效因子后,如何把这些有效因子进行组合;主观股票也类似,如基金经理具备跨风格管理能力,其组合夏普将天然优于单一风格产品。
为什么要做组合?
很多时候大家只是模糊觉得组合能提升夏普,至于为什么组合能提升夏普,多数时候却回答不上,今天我们就通过数学的方式把这个简单的道理讲明白。
假设我们找到两个子策略,其长期的风险收益特征均是“年化收益20%、年化波动率20%”,按照夏普的定义,在无风险利率为0的情况下,这两个子策略的夏普均为1。

其中,Rp是策略的年化收益率,Rf是无风险利率,σp是策略的年化波动率。
问题:当组合等权持有这两个子策略时,组合的年化收益率、年化波动率以及夏普分别是多少?
如果你的答案依然是年化收益20%、年化波动率20%、夏普1,那么恭喜,理解不到位。出现偏差的地方来自于对组合年化波动率的理解。
组合后波动率的计算公式如下:
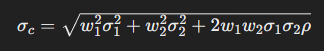
其中,σc是组合的年化波动率,w1和w2是两个子策略的权重,均为0.5,σ1和σ2是两个子策略的年化波动率,均为0.2,ρ是两个资产之间的相关系数
注意看,当两个子策略的相关系数发生变化时,组合夏普会出现怎样的变化:
- 当ρ=1时,σc=20%,即组合夏普为1
- 当ρ=0时,σc=14.14%,即组合夏普为1.414
- 当ρ=-1时,σc=0%,即组合夏普趋于无穷大,当然此种情形在现实世界是极为罕见的
看到这想必大家便能了解,为什么我们在现实的组合管理中,要竭尽全力去追求策略和因子的低相关甚至是负相关。低相关性是上天赐予每一位投资者的宝藏,大家要利用好这个特性,不要动不动就想着去梭哈/择时。
通过上面的简单组合,我们就能把两个夏普为1的低相关资产,将组合后的夏普提升至1以上。
当组合配置的子策略从两个扩展至多个后同样适用,进一步关注的便是两两相关系数(类似于协方差)的问题。
留意相关性共振提升的尾部风险
从上面的推导可以看出,低相关资产进行组合是能显著改善夏普表现的。但反过来,我们在设计和运作高夏普策略时,千万要留意杠杆的风险,不要看到高夏普就可以随意上仓位。
仍以上面案例为例,即便两类子策略长期的相关系数是0,一旦出现尾部风险导致相关系数共振提升时,短期夏普将快速下降,这种情况没处理好是会发生爆仓风险的。这便是为什么我一直不建议大家通过放大杠杆做低波动的高夏普策略来实现高波动高夏普。
任何高杠杆下的高夏普策略必然是脆弱的。比如优先劣后的低波FOF,高杠杆的截面类CTA、DMA量化中性等等。
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
