作者:量化君也
题图:量化君也微信公众号
上周给大伙儿介绍了桥水基金的全天候策略,在确定每个资产权重时提到了风险平价(Risk Parity)这个概念,有些小伙伴说看不懂它的计算步骤,那好的,今天咱来唠唠风险平价。
风险平价这个概念是磐安基金(Panagora)的钱恩平(Edward Qian)博士在2005年提出的,在论文《Risk Parity Portfolios: Efficient Portfolios Through True Diversification》中有一个生动形象的例子。

在股债组合中,股票资产的权重是60%,债券资产的权重是40%,看上去资金是分散了,但实际上风险并没有有效分散,90%以上的的风险都集中在股票端。
具体是怎么得出这个结论的呢?咱来仔细计算一下~
股票端(Russell 1000 Index)的年化波动率是15.1%(标准差),债券端(Lehman Aggregate Bond Index)的年化波动率是4.6%,它俩的相关系数是0.2。
那么,整个组合的方差波动率就是:
(60%)^2 × (15.1%)^2 + (40%)^2 × (4.6%)^2 + 2 × 60% × 40% × 0.2 × 15.1% x 4.6% ≈ (9.6%)^2
其中“x^2”表示的是x的平方,股票端贡献的方差波动率就是:
(60%)^2 × (15.1%)^2 + 60% × 40% × 0.2 × 15.1% x 4.6% ≈ (9.24%)^2
那么股票端的风险贡献占比就是(9.24%)^2 / (9.6%)^2 = 92.64%,也就是说,股票端的资金权重虽然是60%,但却贡献了将近93%的风险,资金权重40%的债券只贡献了7%的风险。这还是在论文当中用收益率方差衡量风险的情况下,如果用常用的标准差,股票端的风险占比更高,高达9.24% / 9.6% = 96.25%。
所以,这就是传统的按资金分配资产权重的问题,风险并没有被有效分散,钱博提出的风险平价就是来解决这个问题的,“风险分散才是真的分散”,每个资产带来的风险应当相同。
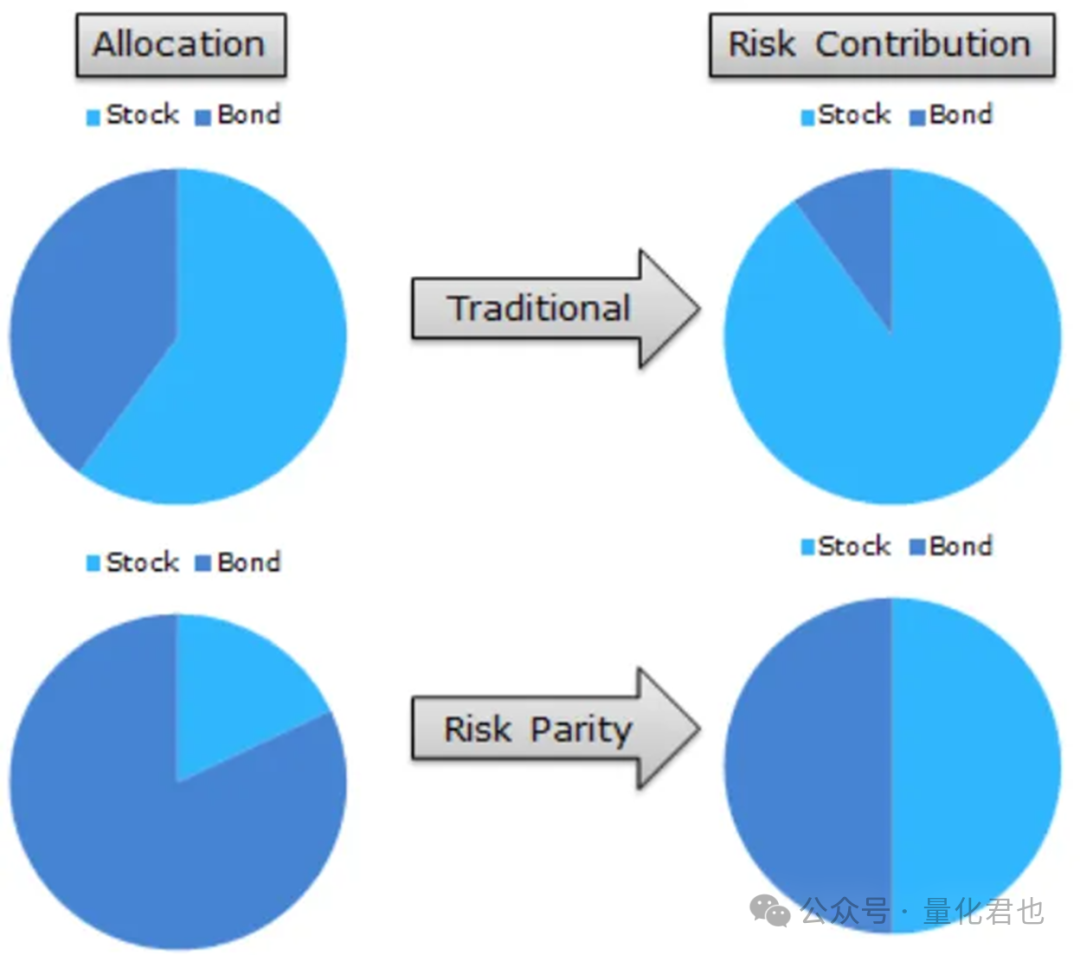
知道了风险平价的理念,那咱就来看看怎么根据风险平价,算出每个资产应该配置的权重。
咱假设投资组合当中有n个资产,第i个资产的权重为wi,第i个资产的收益率为ri,那么资产的权重向量(列向量)就是w=[w1, w2, ..., wn],那么资产组合的收益就是rp = w1*r1 + w2*r2 + ... + wn*rn,资产组合的波动率(代表风险)就是:
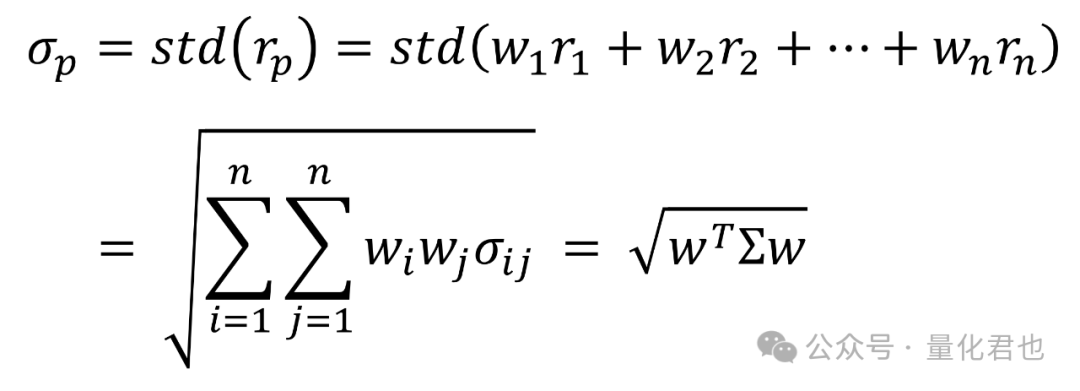
其中σij表示资产i和资产j之间的协方差cov(ri, rj),σij=σji,特别地,当i=j时,σii = cov(ri, ri) = variance(ri) = σi^2,也就是资产i的协方差等于其本身的方差。
std(x)表示求x序列的标准差,Σ表示协方差矩阵,其中第i行第j列的元素就是σij,长下面这个样子。

接下来就是要计算边际风险贡献MRC(Marginal Risk Contribution),它的金融意义就是对应资产权重wi变动1单位时,资产组合波动率σp变动多少,对σp求偏导。
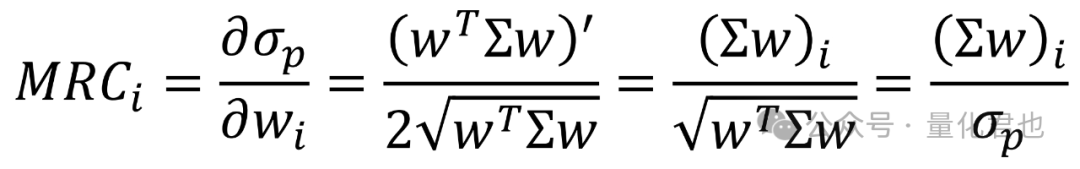
那么资产i对总风险的贡献TRC(Total Risk Contribution)就是权重wi与边际风险贡献MRCi的乘积。
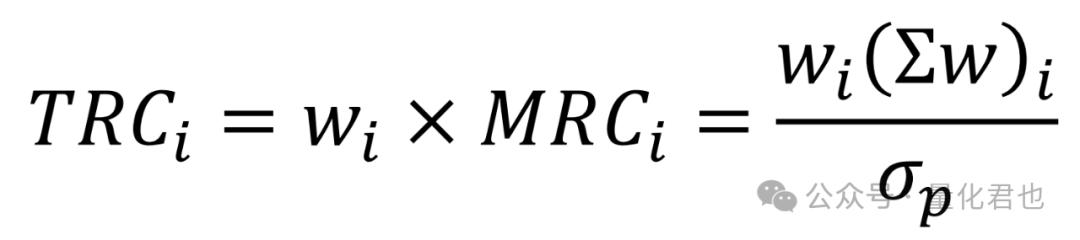
风险平价的目标就是让各个资产对组合总风险的贡献程度就是一样的,也就是TRC1 = TRC2 =…= TRCn,那么求解最优的权重w就可以转化为求解以下最优化问题。
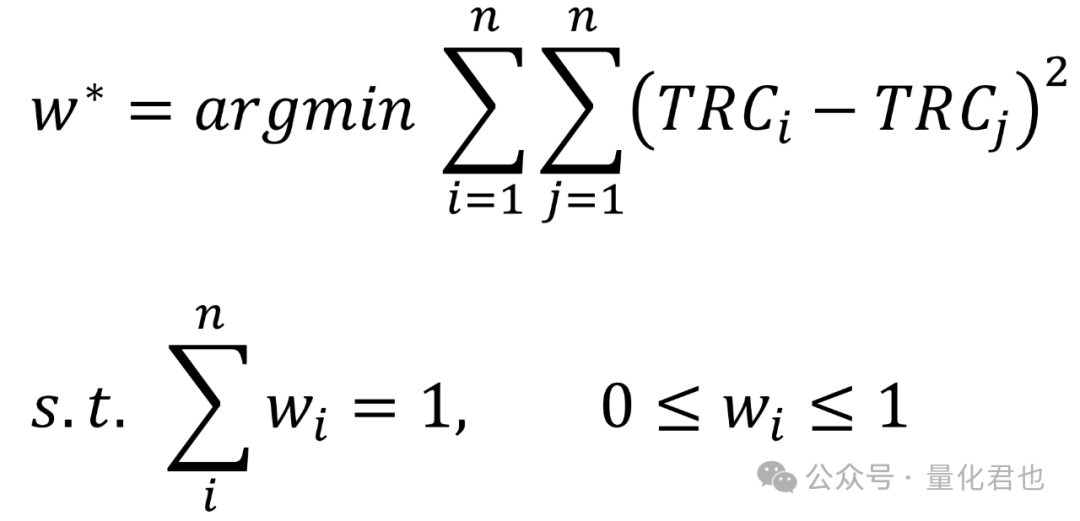
因为在现实当中,是很难让每个资产的TRC相互之间完全相等的,只好让它们之间的相互差值的平方之和最小,也就是让它们之间尽量靠近,这种最优化问题用scipy库当中的minimize函数就非常容易求解了。
数学推导说完了,风险平价到底有没有用,是骡子是马,咱牵出来溜溜。
上周的躺平版全天候策略用的是Dalio给出来的固定权重,咱这次就沿用相同的持仓,但持仓的权重用风险平价理论每一期动态确定,持仓列表如下。
股票类:沪深300ETF,中证500ETF,标普500ETF,纳指ETF;
中期债券:5年期国债ETF;
长期债券:10年期国债ETF;
黄金:黄金ETF;
大宗商品:大宗商品ETF。
为了能与之前的躺平版全天候策略进行对比,设置相同的回测时间范围、调仓周期、费率和滑点等等,先将之前的回测绩效po上来。
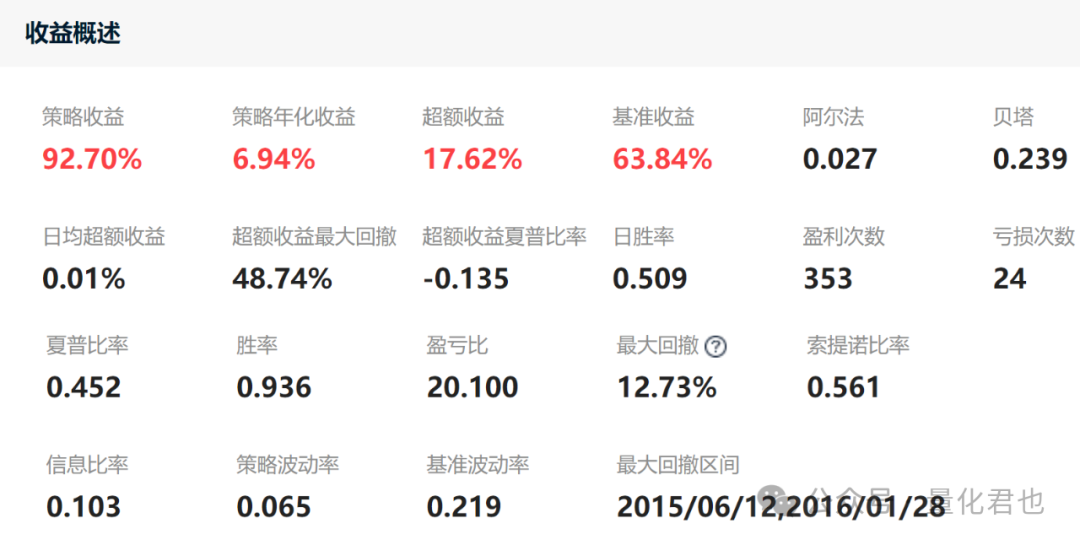
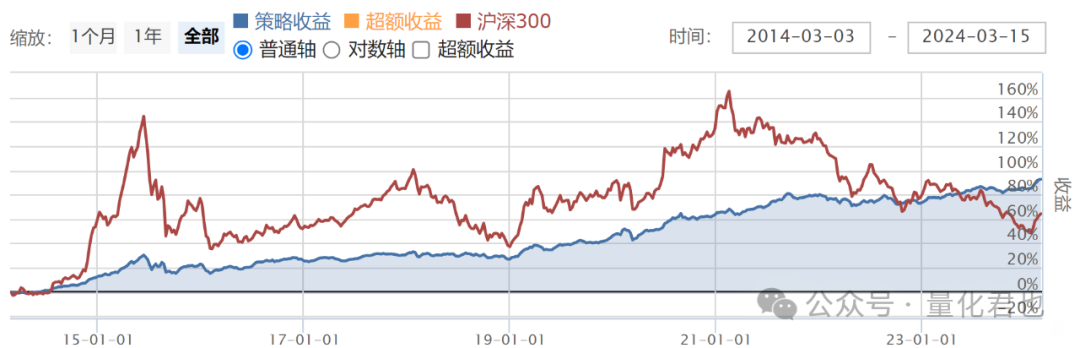
再回测本次的风险平价策略,回测绩效如下。
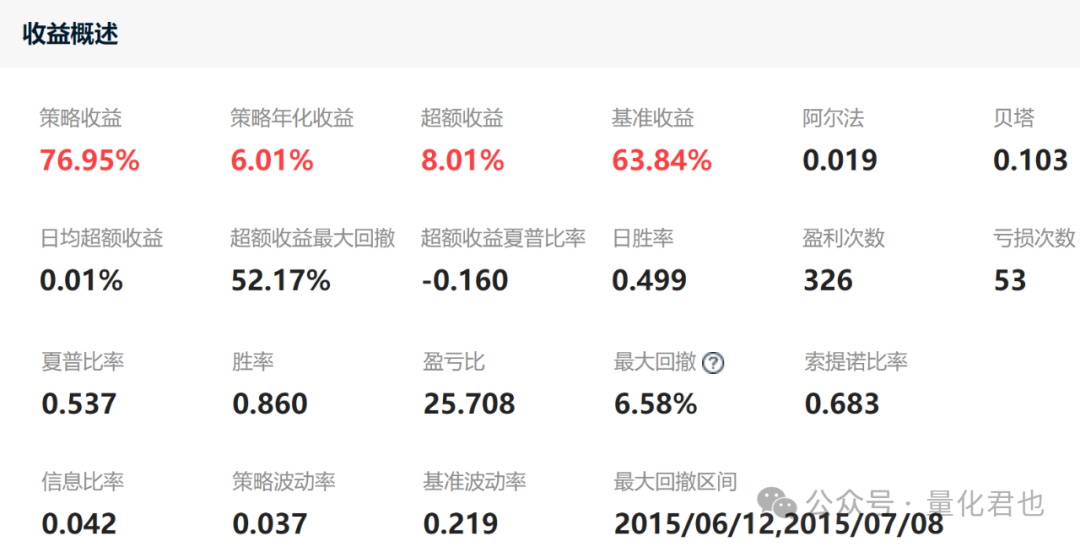
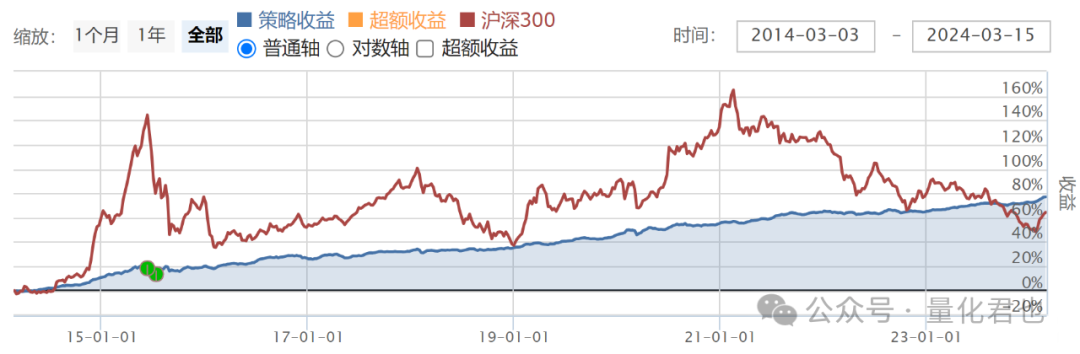
从两者绩效对比中看出,风险平价策略年化收益是6.01%,躺平版策略年化收益是6.94%,年化收益下降将近1%,收益虽然下降了,但夏普率却提高了,之前的夏普率是0.452,现在却上升到了0.537,这主要归功于风险平价对风险的分散/控制能力。
从净值曲线上也可以明显看出区别,风险平价策略的净值曲线要更加平滑,看向具体的数值,现在的最大回撤是6.58%,跟之前的12.73%比起来差不多就是直接减半了,现在的策略波动率是0.037,之前的策略波动率是0.065,降幅也达到了43%。
看出来了吧,风险平价还是有用的,但它不是用来提高收益的,反而会降低收益,它的最大用处就是分散/控制资产组合的风险,有效降低资产组合的波动率和最大回撤,提高策略的收益风险比,有更好的持仓体验。
在量化实践中,风险平价可以当成是一个用来确定组合权重的策略模块,比方说你选股选币选期货、选ETF选基金,选出你想要的那一篮子后,就可以用风险平价确定篮子里面每一个品种的权重,还是押注同样的Alpha风格,但降低了持仓的波动和风险,就会有更好的收益风险比和持仓体验。
这也是本次策略试验代码当中,我没有把风险平价确定ETF权重的具体逻辑在交易函数当中嵌套实现的原因,而是将它独立成一个单独的函数,输入的参数只有一个,就是收益率的DataFrame,index是日期,columns是品种代码/名称/编号,values是涨跌幅/收益率,这样,无论将来是在哪个量化平台,无论是第三方的还是自建的,只要用的是Python,那就可以直接用这个风险平价函数求解资产权重,搭配各个策略,开箱即用,岂不快哉!
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
