作者:AtraderX
题图:AtraderX微信公众号
引子
今年以来,三十年期国债ETF(511090)涨幅超过8%,基金份额从350万份增长到1500万份,市场对它一直热情不减。我们不仅好奇,它大涨的基础是什么?现在还能买吗?每次我一买就下跌的宿命能打破吗?除了闭眼咬牙买,有没有更好的方式进行交易?
图1:国债ETF基金份额规模(万份)
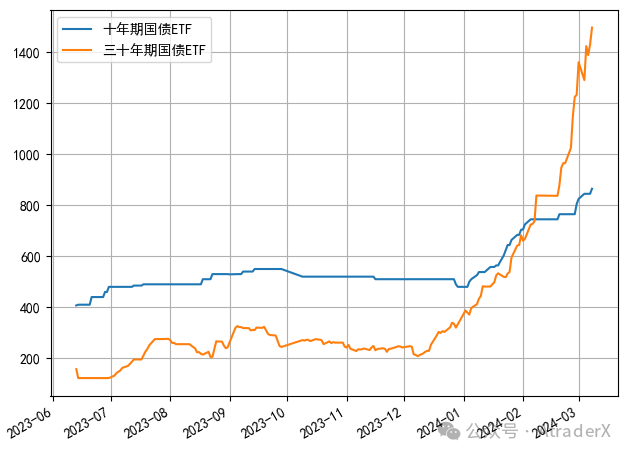
正文首先将国债收益率置于我国的利率体系中,让大家一眼看清国债价格的独特走势。第二部分,我将利用大类资产配置的框架,利用风险平价构建组合的方式,为国债持有者,或潜在买家,提供一个投资国债的思路。
一、国债价格一枝独秀
图2:三十年期国债ETF价格
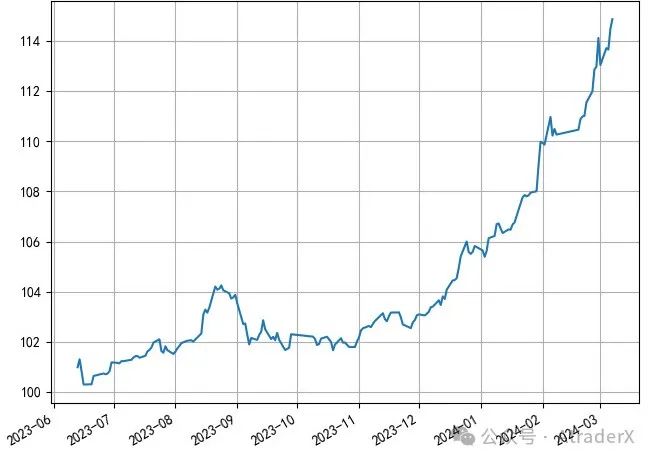
三十年国债ETF今年以来升幅达到8.48%,升势凌厉,颠覆了大家对债券走势稳健的传统认知。即使我们努力分析三十年国债大涨的原因,包括
- 资产荒,
- 经济基本面比较差,CPI,PPI,M1等数据不达预期,
- 国家筹划发行超长期国债,等等
也难以充分解释三十年国债价格的异常强势,市场不乏用“疯狂”来形容它过去两个多月的表现。
将国债价格上涨置于我国的利率体系中分析,我同样惊叹于它的一枝独秀。从图3我们能看到,政府直接调控的是7天逆回购利率和MLF利率,这两个利率进而会影响DR007,LPR和国债收益率。
图3:我国利率体系和调控框架
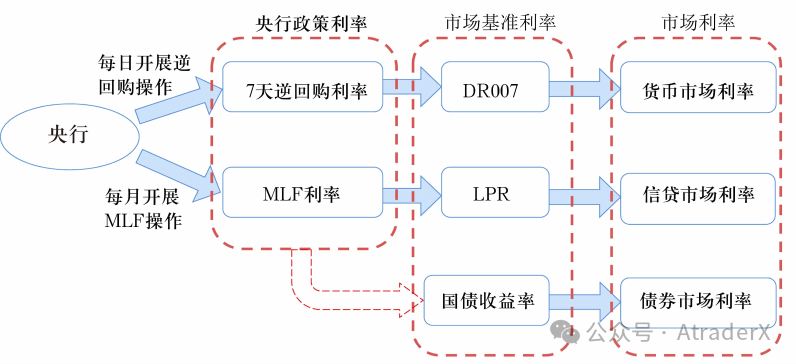
图片来源:《中国的利率体系与利率市场化改革》,易纲http://www.pbc.gov.cn/goutongjiaoliu/113456/113469/4351958/index.html
7天逆回购利率:央行跟商业银行之间的回购利率,央行定价。
MLF利率:央行跟商业银行之间的中期借贷利率,央行定价,期限3个月~1年。
易纲:前央行行长。他的《中国的利率体系与利率市场化改革》一文,逻辑清晰,文字亲民,是非常棒的入门我国利率体系的文章,强烈推荐!
图4到图6是市场基准利率中三个利率的走势。三个利率中,DR007和LPR在2024年保持稳定。LPR在MLF利率的基础上进行加点,MLF利率2024年维持不变,LPR加点变化不大,所以LPR同样维持稳定。国债利率却大幅下滑,最新十年国债和三十年国债的利率都已经低于2.5%。
图4:2024年DR007走势
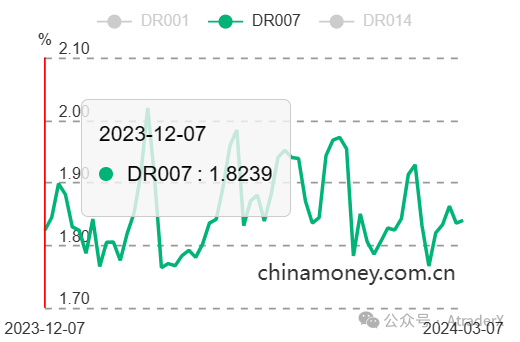
数据来源:中国货币网
https://www.chinamoney.com.cn/chinese/mkdatapm/?tab=2
图5:一年期中国MLF利率
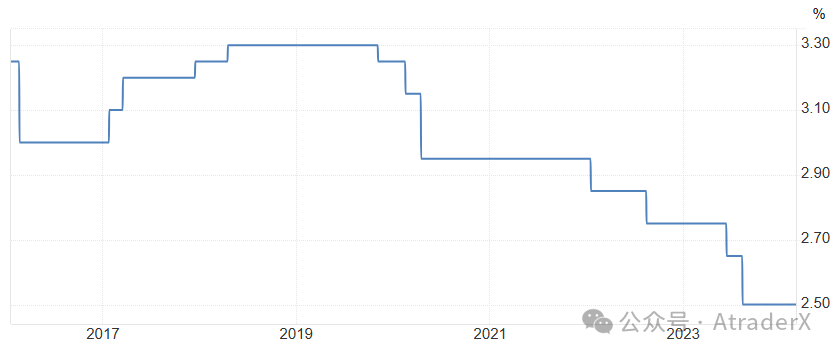
数据来源:tradingeconomics.com
https://zh.tradingeconomics.com/china/1-year-mlf-rate
图6:中国三十年期国债收益率
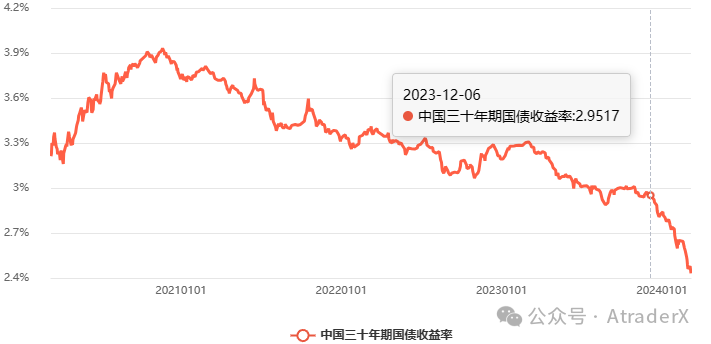
数据来源:macroview.club
https://www.macroview.club/data?code=cn_bond_30year
除了发出“疯狂”的惊叹,我想大家更关心的应该是国债ETF后续的走势?特别三十年国债ETF。这个问题的本质是问国债ETF还能买吗?
非常坦诚地告诉你,如果仅关注国债的价格,我也没有答案。但是,我们可以将思路打开,从股债平衡的角度,或者资产配置的角度思考这个问题。
二、在大类资产配置框架中思考国债合理持仓
所谓股债平衡或者大类资产配置,就是构建多资产组合,各类资产的涨跌有望互相弥补,进而提升组合的收益或者降低组合的波动。
为了对冲国债的波动,我们可以考虑买入股票。我们假设这样一种情景,2月份的经济数据超预期,比如M1增速超预期回升,这有望刺激A股上涨,而刺激经济的预期减弱,国债可能走弱。如果M1增速重回低迷,A股下跌而国债走强,两者也会互相抵消。在这情景里,A股和国债将互相弥补,从而降低组合的波动。
表1:股债互补情景假设

假设我们的组合就持有A股跟国债,资金要如何分配呢?
表2:股债组合权重分配

将资金平均分配不是好主意,因为股票的波动将主导组合的波动。通过历史数据,我们可以计算A股和国债的波动率。从图7可以看出,股票的年化波动率远超国债的波动率,通过计算,前者的平均值大约是后者的7倍。
图7:年化波动率
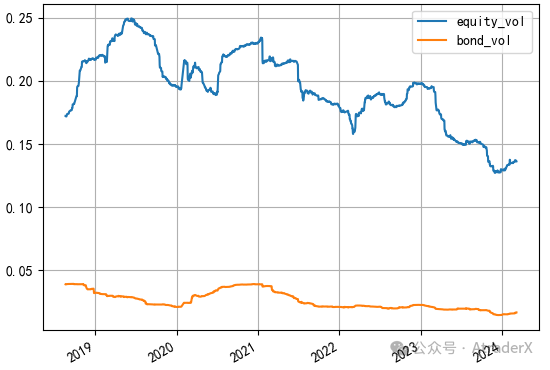
为了实现A股和国债往组合贡献的波动一样大,我们设定两个条件:
equity_w + bond_w = 1 (1)
equity_vol * equity_w = bond_vol * bond_w (2)
w 代表权重,equity_w 和 bond_w 是我们需要求解的资产权重。vol 代表波动率,equity_vol 和 bond_vol 是提前计算好的股票和国债的波动率。
等式(1)变形
bond_w = 1 - equity_w
代入等式(2)得到
equity_vol * equity_w = bond_vol * (1 - equity_w)
equity_vol * equity_w = bond_vol - bond_vol * equity_w
equity_w * (equity_vol + bond_vol) = bond_vol
equity_w = bond_vol / (equity_vol + bond_vol)
计算得到 equity_w 后,
bond_w = 1 - equity_w
求解计算,画图,以及构建组合的代码在文末,需要的请转到文末。
图8: 组合中股票和国债的权重(求解所得)
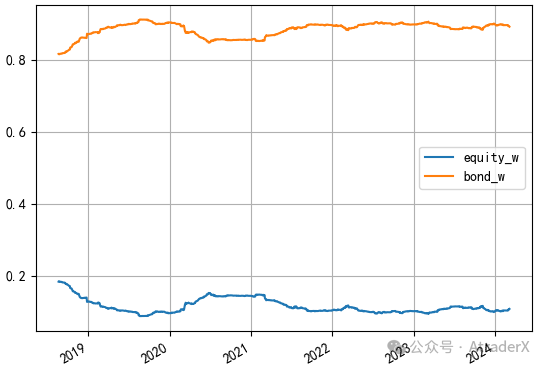
由于股票的波动大,它在组合中的权重就小,国债波动小,权重就大。通过计算,国债在组合中的权重大约是股票的7倍。通过权重的调整,股票和国债往组合贡献的波动水平就是相等的。图9中有两条线,分别是国债和股票往组合贡献的波动,只是它们完全重叠了,所以看起来像是只有一条线。
图9: A股和国债往组合贡献相等的波动
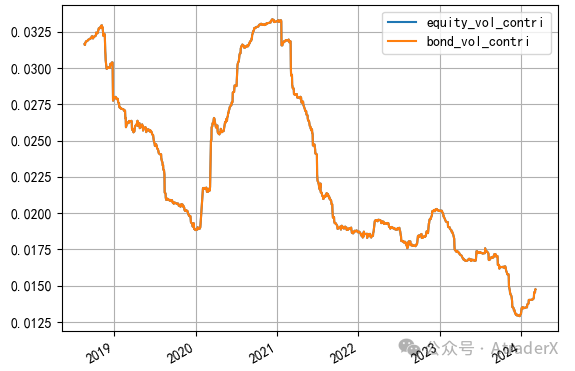
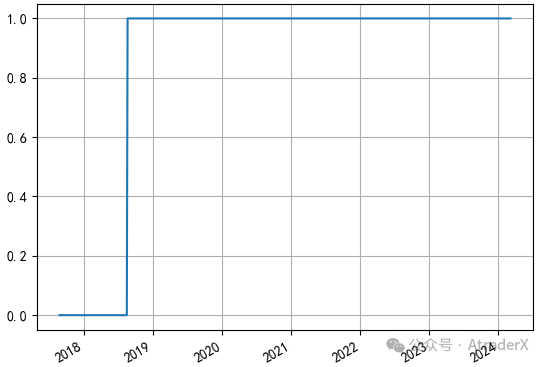
图10: A股和国债权重之和
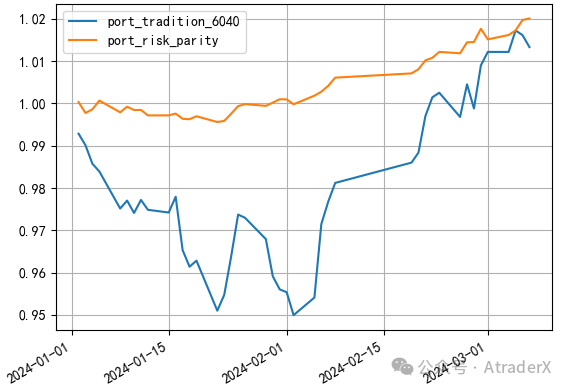
各类资产往组合贡献相等的波动,这就是所谓的风险平价。用风险平价的方式构建组合,股票和债券往组合贡献相同强度的波动,避免了单一资产的主导组合波动的风险。我们可以看图11种两个组合的差异。橙色线是用风险平价构建的组合,它的波动和最大回撤都优于传统的股票60债券40组合。
图11: 沪深300ETF和十年期国债ETF组合
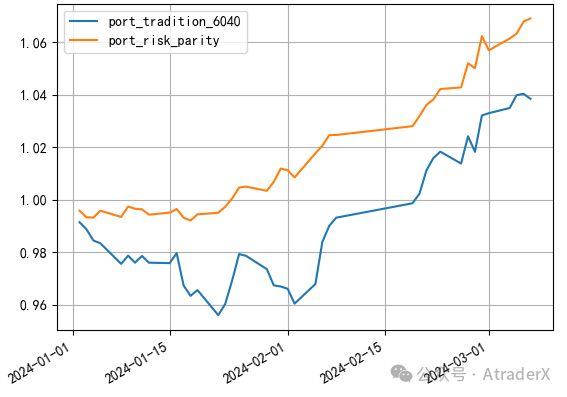
如果我们用三十年期国债ETF取代十年期国债ETF,收益会更高,如图12。
图12:沪深300ETF和三十年期国债ETF组合
结束语
本文介绍了用风险平价的方式构建组合。我只用到股票和国债两类资产,如果我们添加更多资产,求解将变得棘手,我们可以调用 python 的 scipy 包,利用它的寻优功能,让计算机去计算各类资产的权重。具体代码可以看我之前的文章《李蓓最大回撤25%,除了围观她的持久战,我们也可以学习宏观平价策略》,寻优的代码被我内置于这篇文章中。
有了大类资产配置的思路,以及构建组合的方式——风险平价,我们就能跳出单一资产投资的限制,不必再纠结某一类资产一时的涨跌。我们可以往组合加入更多类资产,比如本文加入了A股。我们可以加入贵金属,比如黄金,有色或者其他商品,我们也可以加入美股。丰富的组合,资产间涨跌互相抵消,将极大降低组合的波动。
当然,不是什么资产都可以随意添加到组合里。我们还是应该遵循相关性低,预期收益为正等几个简单的条件来为组合挑选大类资产,具体的例子我们留到日后吧。
# 构建组合所用代码
import pandas as pd
import numpy as np
import matplotlib
matplotlib.use('Qt5Agg')
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
plt.rcParams['axes.unicode_minus'] = False # 显示负号
# 十债ETF:511260,三十年期国债ETF:511090,沪深300ETF:510300
# ETF 开高低收数据来自 tushare pro
ETFs = {'equity': '510300', 'bond': '511260'}
# 三十年期国债ETF数据不多,用120天,即过去半年来计算波动率,
# 如果是511260,则用240天
if '511090' in ETFs.values():
ann_trade_dates = 120
else:
ann_trade_dates = 240
fix_ann_trade_dates = 240 # 转化为年化波动率用固定的240天
dfport = pd.DataFrame()
for k, v in ETFs.items():
dfetf = pd.read_csv(
'd:\\work_data\\ETF daily ohlc\\%s.csv' % v,
parse_dates=['datetime'],
index_col='datetime'
)
dfport[k+'_pch'] = dfetf['close'].pct_change()
dfport = dfport.dropna()
dfport = dfport.sort_index()
dfport.index.name = ''
# 传统股票60%,债券40%组合
dfport['port_tradition_6040'] = \
dfport['equity_pch'] * 0.6 + dfport['bond_pch'] * 0.4
# 构建组合的第二种方式:用波动率计算权重,波动大的权重小,波动小的权重大
# 计算波动率, 年化波动率
for k in list(ETFs.keys()):
dfport[k + '_vol'] = dfport[k + '_pch'].rolling(
ann_trade_dates).std() * np.sqrt(fix_ann_trade_dates)
# 计算权重
# setting1: equity_w + bond_w = 1
# setting2: equity_w * equity_vol = bond_w * bond_vol
# calc equity_w
# equity_w * equity_vol = (1 - equity_w) * bond_vol
# equity_w * equity_vol = bond_vol - equity_w * bond_vol
# equity_w * (equity_vol + bond_vol) = bond_vol
# equity_w = bond_vol / (equity_vol + bond_vol)
dfport['equity_w'] = dfport['bond_vol'] \
/ (dfport['equity_vol'] + dfport['bond_vol'])
dfport['bond_w'] = 1 - dfport['equity_w']
dfport['equity_vol_contri'] = \
dfport['equity_w'] * dfport['equity_vol']
dfport['bond_vol_contri'] = \
dfport['bond_w'] * dfport['bond_vol']
# dfport[['equity_vol', 'bond_vol']].plot(
# title='波动率', grid=True)
# dfport[['equity_w', 'bond_w']].plot(
# title='权重', grid=True)
# dfport[['equity_vol_contri', 'bond_vol_contri']].plot(
# title='Vol Contribution', grid=True)
# dfport[['equity_w', 'bond_w']].sum(axis=1).plot(
# title='Total Weight', grid=True)
# 计算组合收益
dfport['port_risk_parity'] = \
dfport['equity_w'] * dfport['equity_pch'] \
+ dfport['bond_w'] * dfport['bond_pch']
# 画图
(dfport.loc[pd.to_datetime('2024-01-01'):,
['port_tradition_6040', 'port_risk_parity']
] + 1).cumprod().plot(title='组合收益', grid=True)谢谢您的阅读!
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
