作者:川总写量化
题图:川总写量化微信公众号
摘要
Portfolio Sort 是实证资产定价和因子投资中的常见方法。本文带你了解 Portfolio Sort 的源起,中兴和未来。
1 源起
资产定价的研究目标是解释不同资产的预期收益率在截面上的差异。为了构造因子、或者为了检验给定的定价模型,选择适当的资产(被称为 test assets)十分关键。在这方面,一个自然的想法是使用 individual assets,比如个股。但是个股层面巨大的 idiosyncratic noise 使得估计得到的 beta 误差很大,造成 errors-in-variables(EIV)等问题。
正因如此,在最早检验 CAPM 的时候,无论是 Black, Jensen, and Scholes (1972) 还是 Fama and MacBeth (1973) 都选择使用投资组合代替个股。具体而言,他们将个股按照其历史 beta 的大小排序,然后构成不同的投资组合,并检验这些投资组合的收益率和 beta 的关系。这背后隐含的逻辑是,个股 beta 的估计误差相互抵消,因此投资组合的 beta 估计值更准确。
这就是最早的 portfolio sort。
2 中兴
然而,真正让 portfolio sort 成为实证研究标配的是 Fama and French (1992, 1993)。Fama 和 French 利用 portfolio sort 分别研究了 size、value 等异象并提出了 Fama-French 三因子模型。颇为有意思的是,在研究异象的时候,股票被分为 10 组;然而在构造因子的时候,股票则是依照市值和 BM 分别被分为了两组和三组(下图展示了 SMB 和 HML 两个因子的构造方法)。

构造因子时的分组数通常小于研究异象时的分组数。这背后的逻辑并不难理解:为了控制市值的影响,构造因子往往使用目标变量和市值独立双重排序。如果每个变量下分的组太多,那么一些投资组合可能就没有足够数量的股票。
作为实证研究的典范,Fama 和 French 开创的传统被自然而然地延续了下来。后续的一众实证研究,在通过 portfolio sort 研究异象时,无不采用 10 组的划分;而当构造因子时,使用的组数则要少得多。John Cochrane 在 AFA 主席演讲时,关于 portfolio sort 曾评价道:

上述选择组数的做法听上去是如此的理所应当,以至于没有谁会质疑它的合理性。然而事实真的如此吗?从数学上说,portfolio sort 其实就是 nonparametric cross-sectional regression estimator。Cochrane (2011) 里面的这张图清晰地表明了这一点。
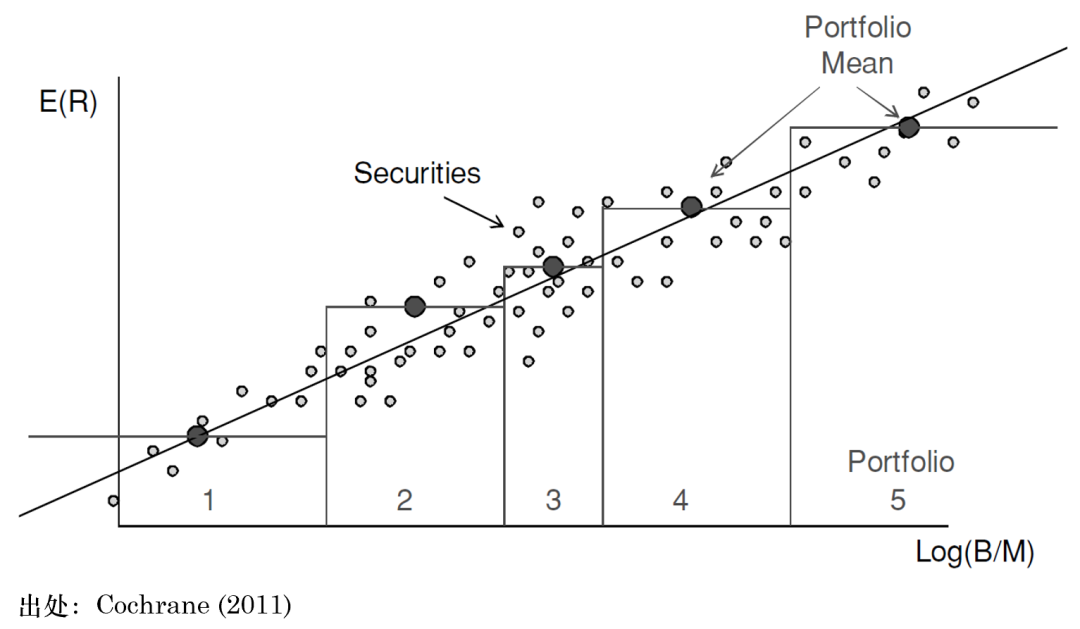
作为一个 nonparametric/kernel estimator,portfolio sort 却是一个非标准化的方法。比如,从 kernel estimator 的角度来理解,每个分组中的 asset 的收益率估计值就由其所在组的所有 assets 的收益率均值决定。然而,portfolio sort 的非标准之处在于临界资产的分组。比如,以上图中的 log(B/M) 为例,如果某个公司的数值稍稍小了一点,那么它就可能被划分到第 1 组,如果它的数值稍稍高了一些,它就会被划分到第 2 组。这种跳变和 kernel regression 中常见的 kernel 完全不同(比如 Gaussian kernel)。因此,尽管 portfolio sort 简单好用且在实证研究中发挥了重要的作用,但人们对它的统计特性却知之甚少。
除了上面提到的问题之外,另一个问题是股票数据是 unbalanced data,意味着截面上的股票个数会随时间会发生巨大的变化。以下图为例,它展示了 CRSP 中所有股票以及 NYSE 上市的股票的数量随时间的变化。就全部股票而言,在 1960 年之前截面上不足 2000 支股票;然后在 70 年代发生了跳变,并在 90 年代上升至将近 8000 支;最近 20 年又逐渐下降至 4000 支。面对如此巨变的截面股票数量,我们不禁要问,忽视股票数量的变化而一直采用 10 分组是否合理?如果不甚合理,那么应该如何确定最优的分组数?这个最优的分组数又是否和截面上的股票数量有关?
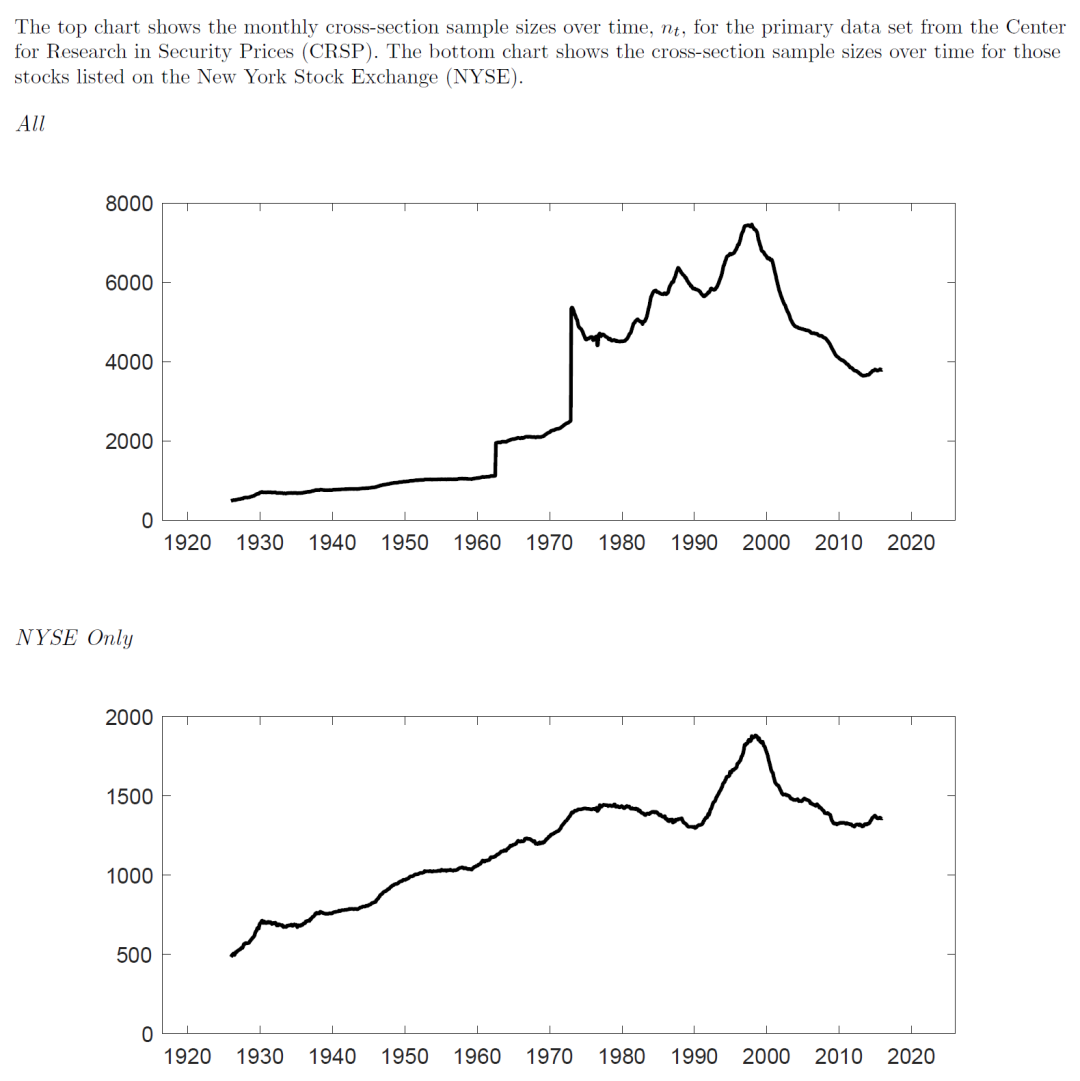
毫无疑问,继承自 Fama and French 的 portfolio sort 承载和见证了实证研究的过去。但展望未来,通过将 portfolio sort 视为 nonparametric estimator,了解其性质,并回答上面提到的那些问题,才代表着实证研究方法的进步。
3 未来
Cattaneo et al. (2020) 对上述问题进行了系统的回答。
该文通过将 portfolio sort 视为一个 nonparametric estimator,提出了一个关于它的估计和推断的通用框架,并介绍了有效的渐近推断方法。它通过最小化估计量的均方误差,为挑选最优分组数提供了理论依据。他们的研究发现,最优的分组数和总的期数以及截面上的资产个数二者皆密切相关。
我们借用该文的图 1 从直觉上理解一下背后的原因。
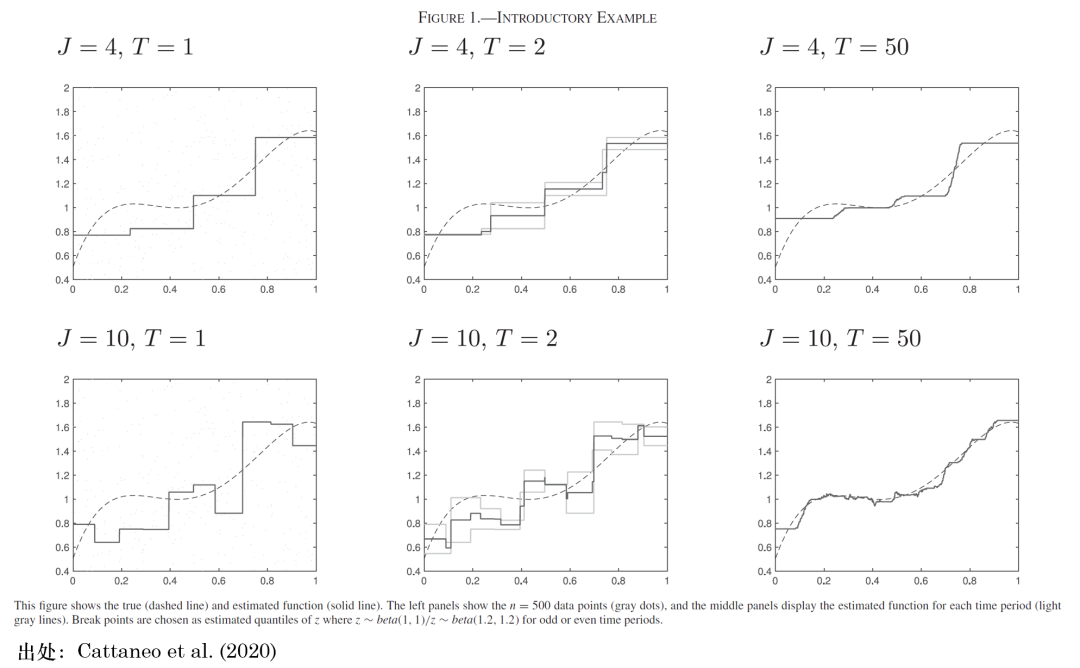

其中 K 是一个依赖于数据生成过程的常数。对应到实证,最优的分组数远大于常见的 10 组这个选择,随截面上 assets 个数不同,最优的分组数的变化范围从数十到上百。值得一提的是,上述公式是对于构造异象而言。对于构造因子,Cattaneo et al. (2020) 给出了一个类似的关系。
在实证方面,该文以 size 和 momentum 为例,对比了他们的方法和传统的分 10 组方法(下图展示了动量的结果,左侧为该文的方法,右侧为常规的 portfolio sort 结果)。从结果可知,1980 到 2015 这个实证区间中,投资于过去的输家所导致的损失在增大:在整个实证区间内,输家组的平均收益率约为 -0.8%,而在 1980-2015 的区间内这个数值下降到 -1.5%。因此,动量因子的空头部分使该因子在这个区间更加有利可图,且这一结论在排除金融危机等情况下依然稳健。反观传统的 portfolio sort 方法,它并不能提供同样的发现。
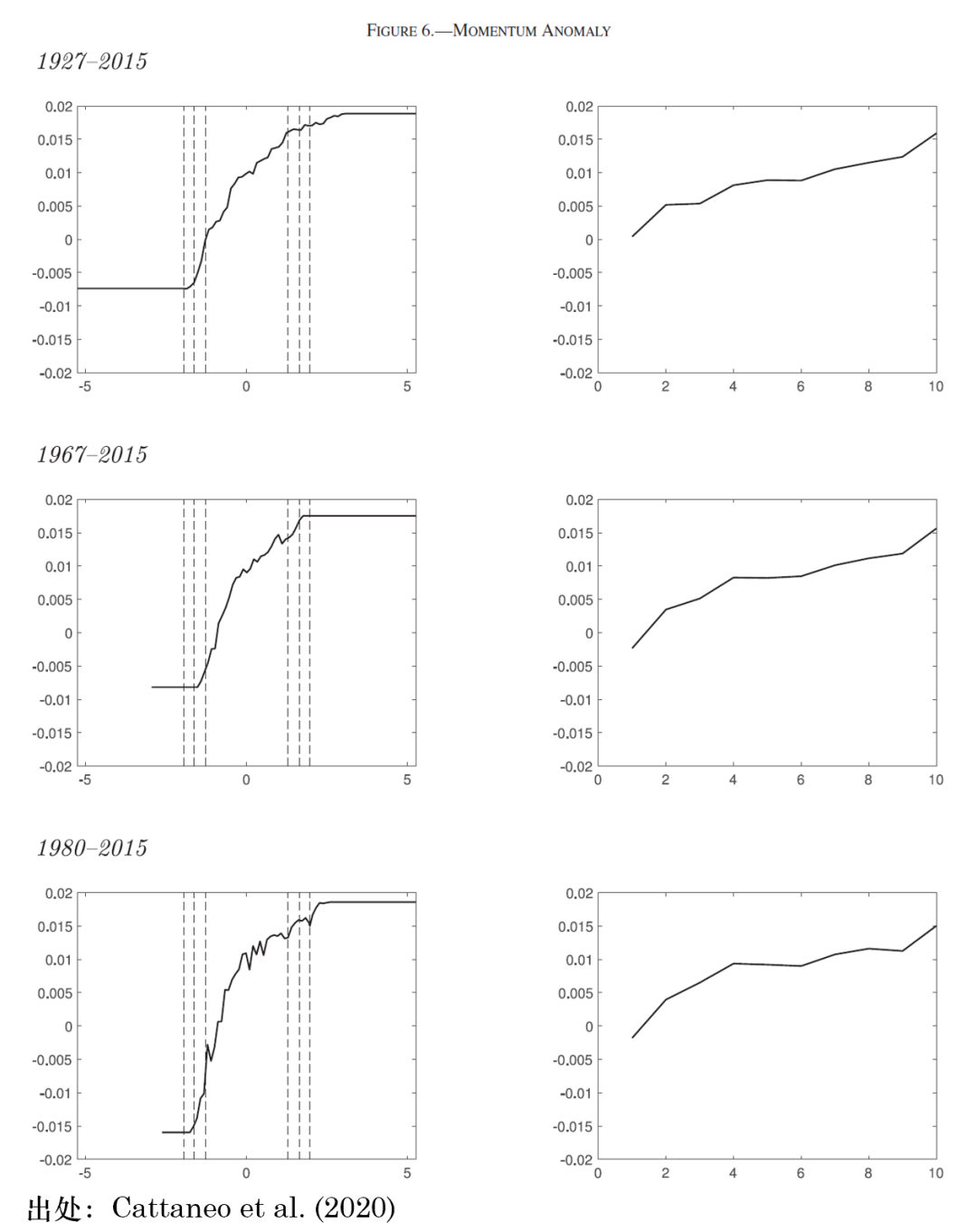
除单变量排序外,Cattaneo et al. (2020) 还对他们的 estimator 进行了扩展,使其可以同时考虑多个变量,进行多变量排序。鉴于双重排序在构造因子时十分常见,这种扩展显得尤为必要。但另一方面,和传统的多变量排序一样,他们的 estimator 也受到维数灾难的影响,即随着用于排序的变量的数量的增加,其性能会下降。为了解决这个问题,他们进一步允许其他条件变量以参数的形式进入模型。这种拓展在 portfolio sort 和 cross-sectional regression 之间实现了一定程度的融合,但又不像纯粹的 regression 那样施加了参数化的假设,因此更加灵活。
无论是构造定价因子,还是构造 test assets 来检验多因子模型,portfolio sort 都至关重要。优秀的 test assets 应该能体现出资产收益率在 cross-section 的差异。从这个角度上说,忽视数据的特征而对所有变量都一视同仁、分成 10 组的做法确实略显粗糙。Cattaneo et al. (2020) 为 portfolio sort 确定最优分组数量提供了一种数据驱动方法,并表明最优分组数量随期数以及截面上资产的个数而变化,为今后关于异象和因子的研究提供了新的启发。
参考文献
Black, F., M. C. Jensen, and M. Scholes (1972). The capital asset pricing model: Some empirical tests. In M. C. Jensen (Ed.), Studies in the Theory of Capital Markets. New York, NY: Praeger.
Cattaneo, M. D., R. K. Crump, M. H. Farrell, and E. Schaumburg (2020). Characteristic-sorted portfolios: Estimation and inference. Review of Economics and Statistics 102(3), 531 – 551.
Cochrane, J. H. (2011). Presidential address: Discount rates. Journal of Finance 66(4), 1047 – 1108.
Fama, E. F. and J. D. MacBeth (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy 81(3), 607 – 636.
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
