作者:量化君也
题图:量化君也微信公众号
 菜场大妈遇上马科维茨,擦出小市值更高收益的火花(十年160倍).mp3
菜场大妈遇上马科维茨,擦出小市值更高收益的火花(十年160倍).mp3
我之前介绍分享过不少量化策略了,但是着重点是在标的筛选和进出场时机的把握,仓位一般都是等权重或是等手数,较少涉及到仓位管理,为了填补这方面的空白,先拿菜场大妈策略下手,唠唠如何在股票清单相同的情况下,通过仓位管理,达到优化策略表现的目的。
先拿菜场大妈策略开刀的原因,是因为它是目前个人宽客非常喜欢的热门小市值策略,但很多公布出来的小市值类型的策略,里面普遍都是对个股进行等权处理,也就是对于筛选出来的小盘股,每支股票都是买入相同的金额,这种处理的确是很方便,但不够圆润,于是乎,盘他!

先给不清楚前情的小伙伴说说菜场大妈选股策略的构建思路,最核心的选股思路归结起来就七个字:质好价低市值小。
质好,就是筛选质量好、基本面好的股票。最初的版本只使用了“股息率”这个因子,能真金白银分红的企业应该不会差到哪里去,后来的改进版本当中,为了筛选更优质的股票,同时使用股息率和PEG因子(市盈率相对盈利增长比率)。
价低,就是筛选质好股票中价格低的股票,最初的版本中是股价不能超过9元,“9元”这个设置除了测试效果好之外,还有一个用意就是,方便小资金的个人宽客使用该策略,买入1手股票加上交易费用和滑点,最多才900块出头,选股10支,还不到1w,真的是非常滴亲民接地气。由于A股最新的“面值1元退市”规则,于是在改进版当中加入了最低限价2元,也就是股价要在2~9元之间。
市值小,顾名思义,也就是筛选出前两步“质好价低”中市值最小的N支股票,作为最终的目标持仓。
您瞧,虽然策略的名称看起来很俗气,但却利用了两个被金融专家孜孜不倦研究的金融异象——小市值和低价股,有明显的盈利逻辑。
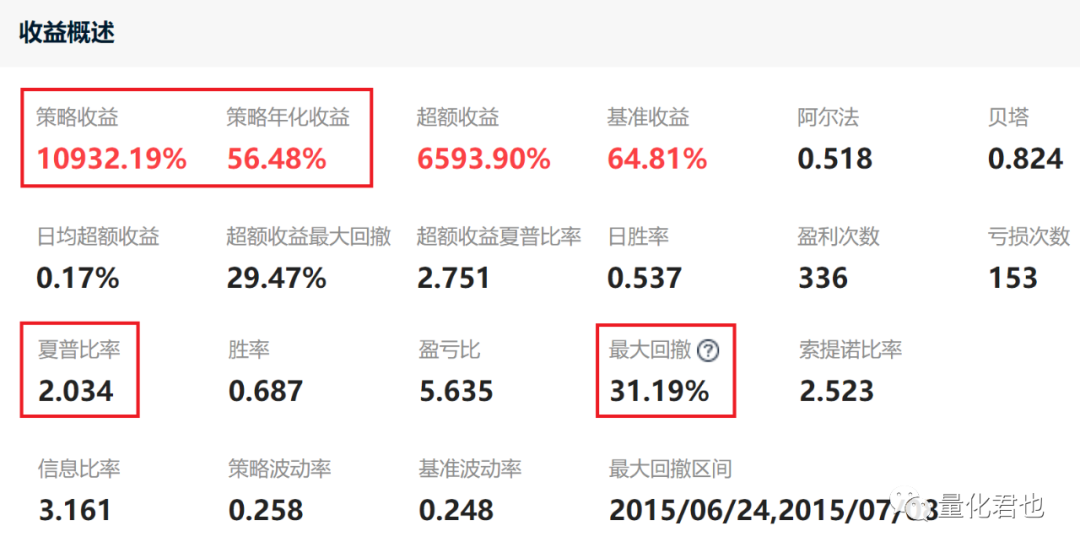
对菜场大妈策略进行回测,每个月第一个交易日调仓,剔除ST、停牌、涨跌停等股票之后,最终选择符合上述条件的10支股票,等权分配资金,正常费率滑点,回测绩效如下,对策略更加详细的描述和回测请见之前的文章《量化交易野路子:菜场大妈选股策略(10年100倍)》。


(对数轴方便看超额收益)
从回测图表中看出,从2013年至今,菜场大妈策略这10年来取得了10932.19%的累计收益,十年100倍,年化收益是56.48%,夏普率是2.03,最大回撤为31.19%,作为一个简单的入门级策略,这个收益情况算是不错的了,而现在,咱想要它变得更好,改进的方向就是仓位管理。
原始版菜场大妈主要解决的是选什么股票的问题,仓位管理解决的是给这些选定的股票如何分配权重的问题。
从解决仓位管理普适性问题出发,假设选股策略选出了n支股票S_1~S_n,给每支股票分配的权重分别是w_1~w_n,假设每支股票未来的预期收益分别为R_1~R_n,那么整个组合的收益可以表示为R=w_1*R_1+w_2*R_2+...+w_n*R_n。

这个组合收益R就是所有仓位管理问题的起点,你希望组合收益呈现出一种什么样的状态呢?是风险一定的情况下收益最高,还是收益一定的情况下风险最小,还是组合里每个股票冒同样的风险,亦或是收益除以风险的夏普值更高~~
要回答这个问题,就要请出现代金融理论和资产组合理论的先驱马科维茨老爷子(Markowitz),马老爷子1952年在其经典之作《Portfolio Selection》提出了均值-方差模型,创造性地将数学引入到金融投资领域当中,从数学层面上解决了资产选择和仓位分配的问题。

马老爷子凭借着对现代金融经济学理论的开拓性研究,以及提供了切实可用的金融资产收益与风险的衡量工具,获得了1990年的诺贝尔经济学奖。可惜的是,马老爷子今年6月在圣地亚哥仙逝了,享年95岁,但留下的理论工具依然熠熠生辉。
咱这次要用到的就是其中的最小方差组合理论,要看懂的话真的不难,只要明白数学期望、方差和协方差的基本定理与性质就可以了。
马老爷子用投资回报的期望值表示组合投资收益率,也就是咱之前已经写出的表达式:R=w_1*R_1+w_2*R_2+...+w_n*R_n;用组合收益R的方差(或标准差)表示组合收益的风险,那将R的式子代入到方差(Variance)的计算公式当中,则可以将式子展开成各个股票收益相关的表达式。
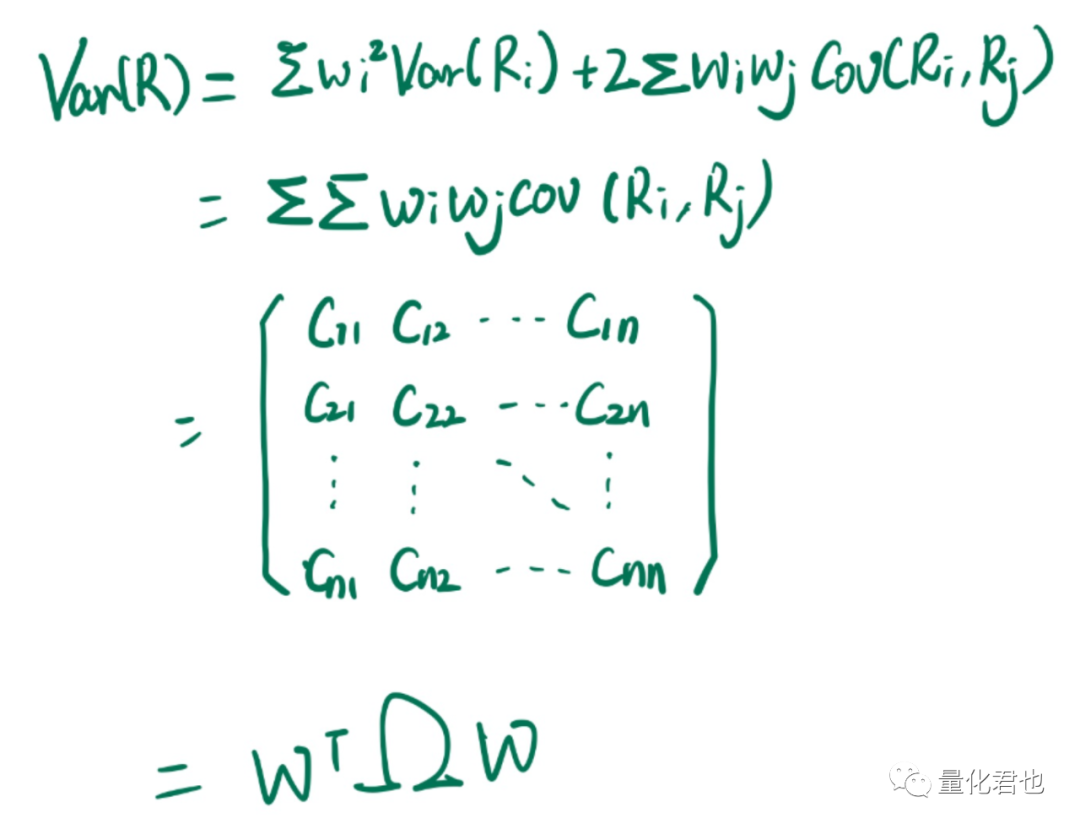
其中Var(R_i)表示第i支股票收益率的方差,Cov(R_i,R_j)表示第i支股票和第j支股票收益率的协方差,特别地,Cov(R_i,R_i)=Var(R_i),如果不明白的话,度娘一下方差和协方差的计算公式就一清二楚了。
于是乎,展开式的第二行就统一用协方差表示,每支股票两两求协方差后与各自权重相乘,最终全部加总。菜场大妈策略是选10只股票,那对应的Var(R)展开是有10x10=100个子项。
为了表达的简洁性,最终表示为向量矩阵的乘积形式,其中W为n维列向量(w_1,w_2,...,w_n),左上角有个T是表示转置成行向量,Ω为股票之间收益率的协方差矩阵(nxn维)。
1xn维的列向量乘以nxn维矩阵,再乘以nx1维行向量,最终的结果是一个标量数值,就是整个组合的风险,咱就是希望找到这个最合适的权重向量W,使得整个组合风险最小化,形成方差/风险最小的投资组合。

怎么找到这个最优权重向量W呢?一般在量化实践当中,咱直接调用数学优化模块进行寻优处理,例如Python当中的scipy库的optimize模块,以Var(R)作为目标函数,给出对应的约束条件,然后它就会给你找出Var(R)最小值对应的那组权重。就跟使用ChatGPT一样,你给它描述任务、背景和条件,它就能给你提供解决方案。
在真正开始实战之前,还要提一嘴最小方差模型的致命缺陷,那就是如果有一个股票之前的股价波动相对较小的话,那它的权重会变得非常大,反之,之前波动大的股票权重会非常小。
用一个例子进行解释,假设有三支股票,为了简单起见,假设它们之间两两不相关,也就是相关系数与协方差皆为0,那收益率的协方差矩阵就是对角元素为各自收益率方差的对角矩阵,那可以显式获得最优权重的解析解。

其中V_i就表示第i支股票收益率的方差(风险),从上面的式子可以看出,股票的权重与其方差成反比,要是股价波动小的话,权重会变得非常高。
如果单纯是根据最小方差组合模型求解权重的话,经常会出现单个股票权重在40%~50%之上,另外一些股票权重在1%之下,如果资金量小的话,低价股也买不进一手,根本成交不了。
所以在量化实战当中,可以人为设定单只个股的权重上下限,指定要在这个权重范围内求解最小方差对应的权重,于是乎,用带权重上下限约束的最小方差组合模型,确定菜场大妈策略每期选出的那10支股票的权重,其他设置不变,重新回测一遍,绩效如下所示。

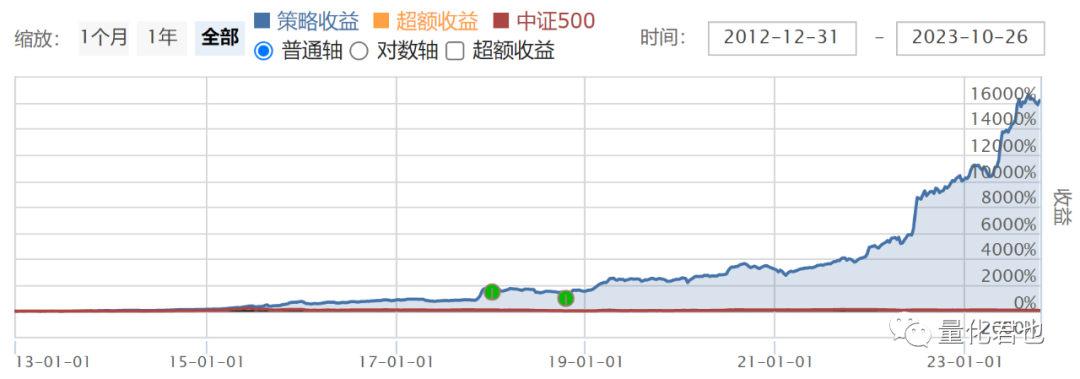

(对数轴方便看超额收益)
年化收益率从56.48%提升到了62.81%,累计收益从十年100倍提高到了十年160倍,夏普率从2.03提高到了2.30,再看看今年年初至今的表现,菜场大妈原版策略目前累计收益是56.61%,马科维茨版的是60.19%,也是高出了一头,说明用马科维茨最小方差组合模型进行仓位分配,还是明显起到了改进策略的作用,没有白折腾。
菜场大妈策略原版:

菜场大妈策略马科维茨版:

细心的小伙伴可能发现了,原版策略的波动率是0.258,最大回撤是31.19%,马科维茨版的波动率是0.255,最大回撤是31.31%,虽然整体波动率是下降了,起到了“最小方差”的作用,但是降低幅度不明显,而且最大回撤还略微增加了,为啥出现这样的情况呢?
那是马科维茨均值-方差模型最最最致命的“缺陷”,在计算组合收益R时,要输入的是股票的“预期收益”,那是未来的事情,或者是咱也不知道股价的真实概率分布,只好使用历史数据代替,过去的波动未必代表未来的波动,就难以起到方差最小化的作用。
但是,如果是同时持仓股票和债券,给这俩分配权重,那很明显,股票与债券的相关性没有股票与股票之间高,并且债券的波动率要明显低于股票,那最小方差模型肯定会将大部分权重给予债券,债券的低波动是持续性的,那就可以起到最小方差的作用,这也从侧面说明了降低整体波动最好是多种低相关资产进行组合。
那马科维茨版的菜场大妈策略为什么会比以前明显收益更高了呢?那是因为长期来看,低波动股票的收益整体要比高波动的股票要高,国内外股市普遍如此,又被称为“低波异象”。

最小方差组合模型更倾向于将高权重分配给低波动股票,对于之前的等权组合而言,相当于是提高了低波动股票的权重,降低了高波动股票的权重,把更多的权重分配给了未来预期收益更好的股票,因此通过仓位管理提高了整个组合的收益。
所以啊,在做仓位管理的时候,也不一定要用马科维茨的模型,只要人为地提高低波动股票的权重,降低高波动股票的权重,也能达到类似的效果,只不过马老爷子的模型算得更合理一些,因为他还考虑了组合股票之间的相关关系,比单独根据波动率因子分配的要强上一丢丢。
以上内容纯粹是个人猜想和探究,用以抛砖引玉,下期见~
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
