对于许多商品品种来说,获得准确、可解释的数据是极其困难的;但幸运的是,商品的期限结构很好地总结了市场已知的基本面。
本文以及之后的关于期限结构的文章中,我们将用量化的方法对期货的远期曲线进行描述,并尝试从几何与形态而非基本面的角度对市场进行分析。
举个栗子
为了更好地理解期限结构的形态对于交易或者策略的影响,我们假设持有单一品种的期货主力合约多头。图一:我们假设在持仓过程中曲线结构保持不变,那么持有一个月的总收益可以认为是升水带来的负展期收益(Roll Return)。
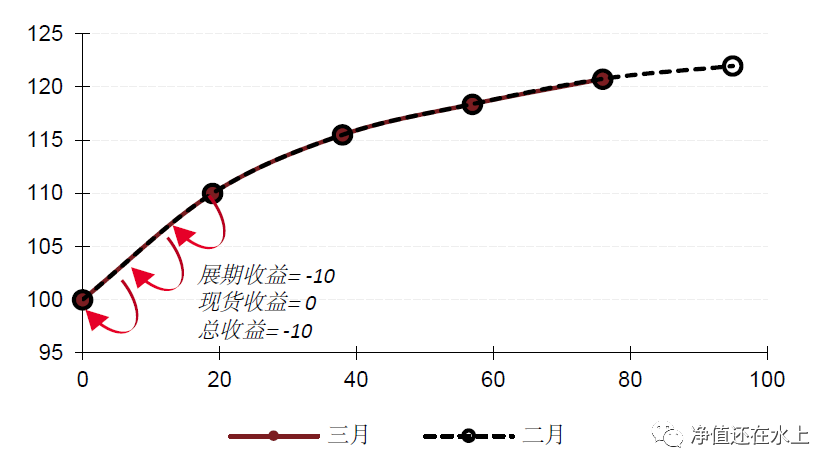
假设从二月到三月,曲线依旧是contango结构,但是近月下跌导致整体曲线更加concave。这种情况下,持仓的总收益 = 展期收益+近月价格变化带来的现货收益。
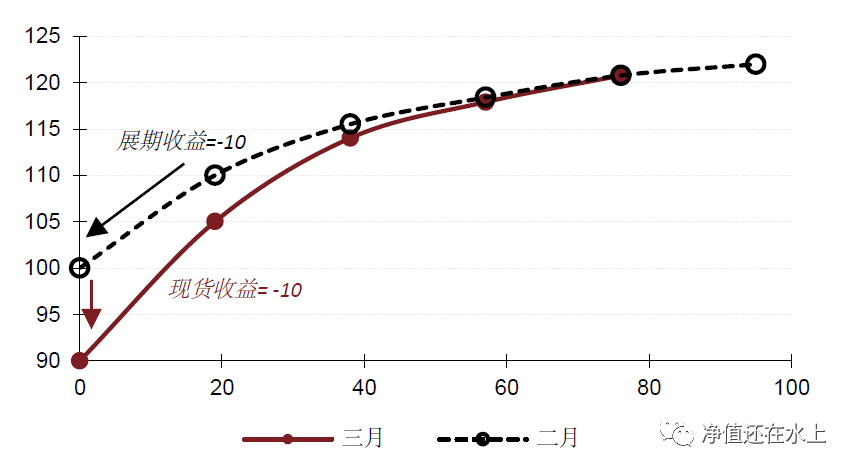
不难看出,曲线形态的变化对于单边持有策略、期限结构截面策略,以及套利策略都有巨大影响。
如何描述曲线的形态
首先,我们将不同到期日的合约价格除以近月价格,
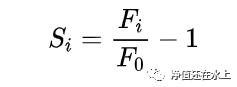
并将计算合约距离到期的时间ti。
Contango vs Backwardation:将相对价格Si对时间ti做回归,
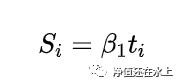
- 如果p值>10%,我们认为无法分类,undefined
- 如果beta_1>0,我们认为目前的结构是contango,否则是backwardation
- Convex vs Concave:同样用价格S_i对t和t^2做回归,
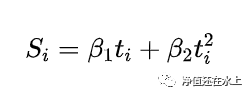
- 如果p值大于合约数量的倒数,我们认为曲线的状态是neutral
- 如果beta_2>0,则是convex,否则是concave
- 根据这种方式,我们可以将期限结构分为以下7种类型:
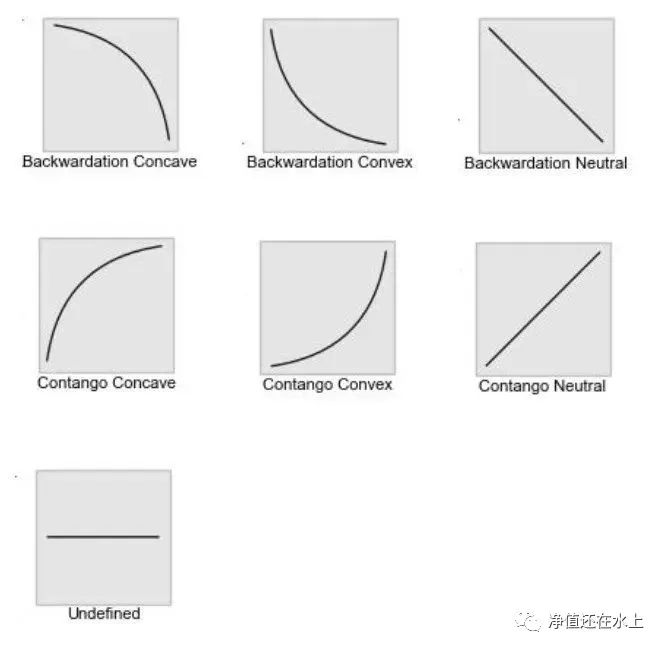
对所有的历史曲线进行分类后,我们可以对每个品种计算这7个状态出现的月度概率。下图中橘色的圆圈大小代表当月某个形态出现的概率。可以看出,螺纹钢的期限结构在16年前后发生的一些明显变化。这是否代表近几年的策略收益中包含了展期收益的影响?

未来我们将研究不同的曲线形态之间的规律,不同状态下量化策略的表现以及与宏观周期的关联。
本文来自微信公众号“净值还在水上”,文章版权归原作者所有,内容仅供参考并不构成任何投资及应用建议
