作者:嘟嘟的投研CheatSheet,好投学堂专栏作家
题图:嘟嘟的投研CheatSheet微信公众号
为何研究净值化雪球?
首先,策略本身有配置意义。作为“高阶版”的网格交易,雪球通过高抛低吸的方式获取了Gamma收益,本身可以作为高波动的独立策略而存在。
其次,净值化雪球允许我们脱离券商交易台。
一方面,“没有中间商赚差价”。券商交易台在对外报价时往往会在理论票息的基础上,打个折扣作为券商的安全垫和利润,净值化则可以吃透这部分折扣。市面上大部分以“滚雪球”命名的私募基金产品,绝大多数便是净值化雪球。
比如75/103 24M/3M结构的中证500雪球,近期券商发售的票息大概在13%-15%;但如果我们自己做净值化雪球,保守按照年化14%的波动率预测,同结构的理论Gamma票息约12.5%,叠加约5%的期指贴水,理论总票息约17.5%,多出来的部分便是券商交易台的销售费用、安全垫以及剩余利润。
另一方面,“万物皆可净值化”。个股、商品甚至Crypto,即便券商没有发行相应品种的雪球,我们依然能通过净值化管理的方式获取票息。像长期看好大饼跟二饼的我,可以通过持有净值化大饼跟二饼雪球来获得额外的票息。
比如与上述结构相同的BTC净值化雪球,按照年化50%的波动率预测,理论票息高达47%。
如何复刻净值化雪球?
第一步,使用蒙特卡洛模拟求解理论票息。
在确定理论票息之前,我们需要先了解雪球是如何定价的。由于雪球属于奇异期权,无法使用传统的BSM公式求解析解,但可用蒙特卡洛模拟估算。
所谓蒙特卡洛模拟法,即先产生N条随机股价路径,用来模拟标的资产在未来的不同行情;然后对每一条路径进行模拟计算,分别在不同的观察时点,判断是否发生敲入或敲出,计算所有路径在雪球到期或敲出时的收益,并按无风险利率贴现最后取平均值,由此得到雪球产品的理论定价。
代码 蒙特卡洛模拟所需参数
# 500雪球理论票息
params=dict(
underlying='CSI500 ABRC', # 合约名称
initial_price = 5400, # 标的资产期初价格
start_date = '20240102', # 合约起始日
end_date = '20251231', # 合约到期日
vd_date = None, # 估值日
monitor=['20240430','20240531','20240628', # 敲出观察日
'20240731','20240830','20240930',
'20241031','20241129','20241231',
'20250127','20250228','20250331',
'20250430','20250530','20250630',
'20250731','20250829','20250930',
'20251031','20251128','20251231'],
k_out_ratios=[1.03] * 21, # 敲出比例,长度需与观察日相同
k_out_prices=[5400 * 1.03] * 21, # 敲出价
k_coupon=0.20, # 敲出票息假设
capital=1, # 名义本金:1百万元
margin_ratio=1, # 保证金率
k_in_ratio=0.75, # 敲入比例
sigma=0.14, # 标的波动率假设,取近3个月年化
q=0.063, # 连续股息收益率假设
r=0.015, # 无风险利率假设,取1Y国债活跃
)
v=simulate(**params)
v比如我们在30万次模拟、75/103 24M/3M结构、每份100万元、年化波动率假设14%、无风险利率假设1.5%、连续股息率假设6.3%、年化票息假设20%的参数设定下,该雪球产品的理论定价为3.73万元。即投资者需支付3万余元才能获得上述结构票息20%的雪球期权。
不过,现实中投资者购买雪球时不会付出额外的成本,因此我们需要测算当票息设定从此前的20%下降到多少时,该期权的理论价格趋近于0时的理论票息,这个过程需要用到二分法。比如按照此前的参数设定,挂钩500的雪球理论票息为12.7%。
欢迎扫码跳转获取完整代码。鉴于实现过程有一定复杂性,代码提供了详细注释,如仍有疑问欢迎在星球提问。不想弄明白过程的朋友也可直接输入参数得出理论定价。
另外,蒙特卡洛模拟算法的求解较为消耗算力,因此也提供了可用GPU加速的Pytorch代码。
# 计算理论票息
theoretical_coupon = calculate_theoretical_coupon(params)
print(f"Theoretical Coupon Rate: {theoretical_coupon}")第二步,使用有限差分法动态求解Delta。
完成定价后,接下来就是解决不同时点究竟要持有多少Delta的问题。
从定义出发,Delta是期权价格对标的资产价格的一阶导数,表示期权价格对标的价格变化的敏感性。
然而直接计算涉及复杂的数学推导,在金融模型中这些导数表达式可能非常复杂或者不可解。因此使用数值差分法是一种简单且有效的近似方法。
在差分法的思想下,我们可以把计算Delta的过程看成是简单测量的过程:
- 小幅调整标的资产价格:假设当前标的资产价格是S,当我们稍微提高价格时,比如S+ΔS,计算新价格下的期权价格V(S+ΔS)
- 计算期权价格变化:我们再把标的资产价格稍微降低一些,比如S-ΔS,计算这个新价格下的期权价格V(S-ΔS)
- 求差值:用两个期权价格的差值V(S+ΔS)- V(S-ΔS)表示期权价格随标的资产价格变化的总变化量
- 计算变化率:用两个标的资产价格的差值2ΔS表示标的资产价格的总变化量,然后用期权价格变化量初一标的资产价格变化量,得到变化率(近似导数),这便是Delta的近似值
## 求解动态Delta
from tqdm import tqdm
import matplotlib.pyplot as plt
import seaborn as sns
import copy
sns.set_theme()
sigma_lst=[0.14]
payoffs,delta,gamma,vega,rho,theta=dict(),dict(),dict(),dict(),dict(),dict()
for sigma in sigma_lst:
payoffs[sigma],delta[sigma],gamma[sigma],vega[sigma],rho[sigma],theta[sigma]=dict(),dict(),dict(),dict(),dict(),dict()
for vd_price in tqdm(np.arange(2700,8100,54)):
p = dict(sigma=sigma,vd_price=vd_price)
params.update(p)
payoffs[sigma][vd_price] = simulate(**params)
for sigma in sigma_lst:
for vd_price in np.arange(2754,8046,54):
delta[sigma][vd_price] = (payoffs[sigma][vd_price+54]-payoffs[sigma][vd_price-54])/(108/vd_price)
for sigma in sigma_lst:
plt.plot(list(delta[sigma].keys()),list(delta[sigma].values()))
plt.legend(sigma_lst)
plt.show()图表 年化波动率为14%时的Delta变化图
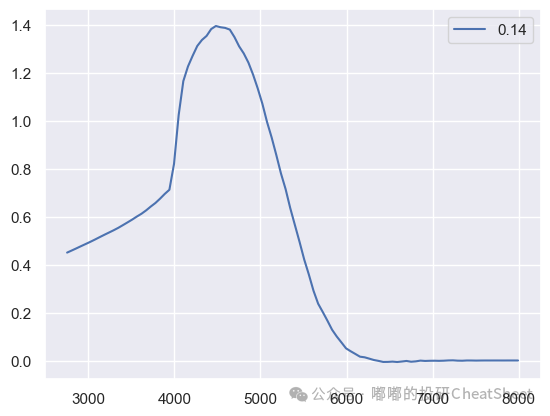
至此,我们便可以通过调整参数,随时根据时间跟价格的变化相应调整Delta。
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
