作者:XYQuantResearch
题图:XYQuantResearch微信公众号
导读
2022年以来,兴证金工团队先后推出了阐述高频研究方法论的《高频漫谈》,以及四篇高频因子深度研究。在高频漫谈中,我们阐述了高频因子的构建逻辑、因子的回测方法以及高频风险的识别。在后续四篇高频因子研究报告中,我们构建了约35个因子,分类涵盖分布和时序信息,其中不乏多个思路新颖、具有较强特异性的因子。
在本文中,我们引入时间、价格和成交量这三类数据,由浅入深地构造关联信息因子。具体来说,我们首先从关联信息在日内全局数据特征出发,从量价的非线性相关性维度出发,引入转移熵刻画量价的关联全局特征因子;之后,我们深入至局部特征,首先刻画出“交易时间”特征,再从交易持续性角度出发构建局部特征;最后,我们尝试挖掘日内具备特异性的典型特征,针对此前的“闪电崩盘”概念和日内“V型”特征构建一系列因子。
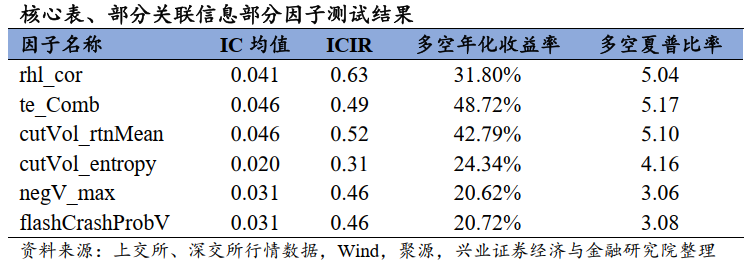
三大类因子在具备选股能力的同时兼具优秀的特异性:在量价非线性相关中,te_Comb因子日度Rank IC均值为0.05,多空收益率约为49%,夏普比率约为5.2,正交后时序相关性均值约为27%,具备较强特异性;在“交易时间”下,基础性因子在算法改造下兼具选股能力和特异性,此外cutVol_entropy因子日度Rank IC均值为0.02,多空收益率约为24%,夏普比率约为4.2,时序相关性均值仅16%,特异性极强;在“V型”走势维度,新“闪电崩盘”具备更强的逻辑性,且具备一定的时序预测能力。
风险提示:模型结果基于历史数据的测算,在市场环境转变时模型存在失效的风险。
1、高频研究回顾与关联信息因子研究框架
1.1高频研究回顾
2022年以来,兴证金工团队先后推出了阐述高频研究方法论的《高频漫谈》,以及《收益率分布因子》、《收益率分布中的Alpha(2)》、《成交量分布中的Alpha》和《时序信息中的Alpha》高频因子深度研究。在高频漫谈中,我们阐述了高频因子的构建逻辑、因子的回测方法以及高频风险的识别。该篇也是我们整个高频系列的基础篇和框架篇,后续所有的研究均建立在此基础上。据此我们介绍了四类高频指标的信息:分布信息、时序信息、关联信息与另类信息。在后续四篇高频因子研究报告中,我们构造了35个高频量价因子,其中不乏多个思路新颖、具有较强特异性的分布和时序信息因子。本文中,我们将聚焦于第三类信息—关联信息。

1.2关联信息简析与因子回测说明
日内股票价格的变动受到多种因素影响,其根本原因是流动性资产供需关系的直接体现。无论出于何种理由,投资者的交易行为会在日内的成交量、买卖单、买卖时点等相关数据上留下“信息”。而由于市场上部分投资者的非理性交易行为,这些信息可能会被视作为领先于股价变动的“先行信息”,进行对投资行为产生影响,并最终反应至股价的未来变动上。在此逻辑下,日内不同维度的量价特征均有可能包含着能够反映未来股价走势的信息。因此,对于流动性资产而言,日内交易数据中的样本数据特征能够作为极其有效的Alpha信息来源。
在高频漫谈中,我们详细阐述了提取日内数据总体分布信息的四种方法。其中,我们定义关联信息需要满意下述定义:
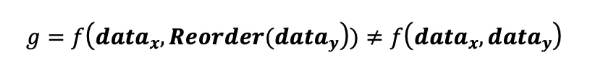
指标 g 对于数据 datax, datay的一一对应关系敏感,改变datax, datay 的对应关系会改变g指标的取值。典型的例子如量价相关性𝛒 (r, volume):改变对应收益率水平下的成交量会极大地改变量价相关性的取值。本质上关联信息是利用了随机变量之间的联合分布关系,同时在金融领域随机变量自身存在着时序特征。在此基础之上,我们衍生出关联信息相关因子。在本文中,我们引入时间、价格和成交量这三类数据,由浅入深地构造因子。具体来说,我们首先从关联信息在日内全局数据特征出发、进一步深入至局部特征,并最后尝试挖掘日内具备特异性和典型性的特征,将三类数据结合使用以构造具有特异性的高频因子。
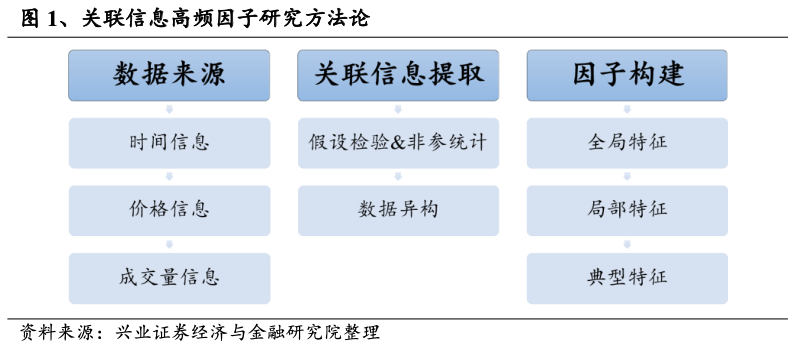
在本文中,针对关联信息的刻画主要有三大重点:数据、特征范围和特征的构建方式。相比于前序的高频因子系列,在本文中我们将引用的数据范围扩大,包括数据的类型(量、价、时)和数据的特征(时序和分布)。这导致本文涉及到的数据复杂度较高。因此,适当的范围限定和合适的数据去噪方式将是因子有效性和特异性的重点决定因素。本文中我们“由浅入深”地展开研究:从关联信息的整体特征出发,逐步推进至信息的局部特征,并最后聚焦于日内某一典型关联特征,从三个角度刻画一系列特异性高频因子。本文的结构如下:
- 首先,我们聚焦于不同日内数据的一阶相关性特征,刻画基础性因子;
- 其次,我们聚焦于日内量价信息的全局特征,从因果关系逐步递推至非线性因果性的刻画,并构建出具有特异性的因子;
- 再次,我们聚焦于日内量价信息的局部特征,先从“自然时间”过渡至“交易时间”,刻画出具备特异性的基础性因子,并最终引入交易聚集性现象,刻画出多个具有特异性的因子;
- 最后,我们聚焦于日内量价信息的典型特征,再次引入“闪电崩盘”的概念,从量、价和时间三维度出发构建日内“V型”特征,并构建出基础性因子和新的“闪电崩盘”概率因子。
2、关联信息基础型因子
2.1因子构建
在上一篇研究报告《时序信息中的Alpha》中,我们从多个维度展示了日内量价数据时序自相关性。其中,在一阶自相关性中,我们通过多种统计量构建了时序基础性因子。在本章中,我们同样聚焦于一阶的相关性信息,但将数据扩展至多个维度。具体来说,我们在本章中通过计算相关系数来刻画多类数据的相关性,包括分钟级收盘价、最高价、最低价、成交量等。由于个股在开盘和收盘阶段的量价信息波动较大,因此,我们均剔除了开盘和收盘10分钟数据。我们尝试下述几种构建方式,作为基础型关联信息因子。

2.2因子表现
我们首先测试上述4个因子的表现。首先从日度IC测试结果上看,大多数的常见关联信息因子IC均值在3%左右,表现出较好的股价预测能力。
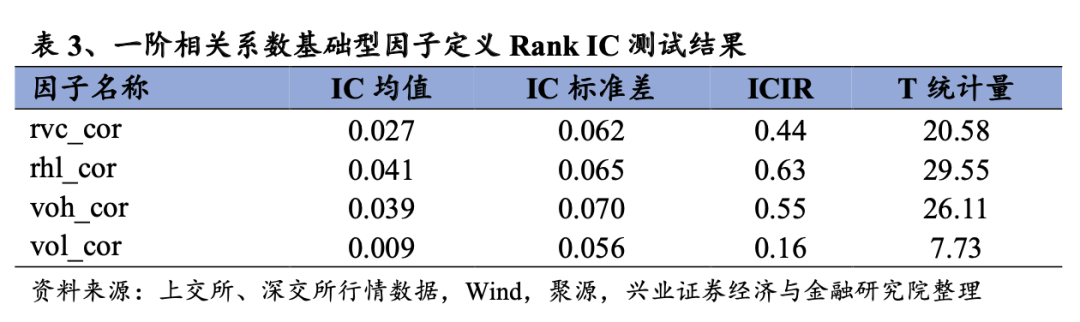
从日度组合测试结果上看,我们构建的一阶相关系数基础型因子的表现均相对优秀,一半因子的多空夏普大于4。具体来看,从多空组合测试上看,voh_cor因子的多空收益率在34%左右,多头收益率高达14%,夏普比率在5.2左右。

3、关联信息中的全局特征:非线性因果关系
在前文中,我们从数据相关性的角度出发,构建了常见的关联信息因子,其重点主要聚焦在对日内信息的一阶相关性的刻画。结果表明,各类因子具有较好的选股能力。上文更多地是从数据统计的角度出发。在本章中,我们将展开特异性因子的第一个部分,也就是通过因果关系刻画关联信息中全局特征:量价因果性。
3.1量价因果性的由来和因果关系的刻画
在股票市场中,股价和交易信息往往是投资者最为关心的两类数据:以成交量作为代表的交易信息代表着流动性资产的供求关系,而股价的变动则代表着由供求关系导致的价格变动。在上述逻辑之中,供求关系的变动往往代表着“因”,股价变动则作为由“因”导致的“果”:市场投资者根据外部信息决定供求关系的变化,进而推动股价变动。然而,在非弱式有效的市场环境,过去一段时间内的量价信息并不完全反映所有的过往信息。因此,大量投资者通过市场的过往量价信息决定未来的交易行为,进而导致“因果倒置”的现象,如“跟风投资”等。在此情形之下,股价的变动则变成为未来供求关系发生变化的“因”。因此,对于非弱式有效的股票市场而言,价格变动和交易信息往往存在着极其复杂的因果关系,对于不同股票而言,其短期内的因果关系往往也存在着较大差异。不同股票的量价因果差异能够从一定程度上反映出投资者对于该股的看法,因此能够成为Alpha信息的重要来源。
在学术界和投资领域,研究者们对于股票量价的因果性有着大量的研究,其中主要分为线性相关性和非线性相关性。其中非线性关系相对复杂且更加难以刻画:两个变量之间的关系不是直线型的,即一个变量的变化不会按比例影响另一个变量的变化,可以用曲线或者其他不规则的形状来描述这种关系。在实际操作中,由于金融数据的噪音程度较高,部分研究已经表明成交量变化率和收益率不存在明显的双向线性相关性(即量的变动幅度与收益率不存在明显的按比例变化的情况)。因此,想要以噪音程度较高的日内分钟数据测算股票自身的量价因果性时,需要考虑更为合适的非线性关系。
3.2线性量价因果性:Granger因果关系和转移熵
在对因果刻画的研究中,Granger因果关系是最为常见的统计方式,用于分析两个时间序列之间的相互影响关系。具体来说,如果时间序列X能够提供统计上显著的信息来预测时间序列Y,并且同时使用X和Y的历史数据对Y进行预测得到的效果要优于单独使用Y的历史数据进行的预测时,那么称X是Y的Granger原因。然而,随着对于变量间关系的进一步认识,研究发现金融序列往往是一种复杂的非线性变化,而传统的Granger因果检验更接近于考察变量间的线性关系,从而会导致研究结论出现明显偏差。现如今,学术界将非线性因果检验的前沿方法归纳为三类:基于回归模型、基于非参函数和基于信息理论。其中,信息理论检验能够从状态转移的角度出发刻画因果性,其对于数据噪音的适应性较强,更加适合用于金融时序数据。转移熵(Transfer Entropy)便是其中的算法之一,其是衡量两个随机过程之间有向信息传递量的非参数统计量,其刻画的是在给定过去状态的情况下,时间序列对于时间序列未来值不确定性的减少量,其具体计算公式如下:
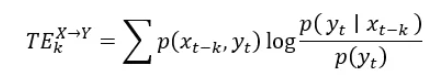
其中, k 为需要主观确定的滞后项,p(xt-k, yt) 是X在时间 t-k 的状态和Y 在时间t的状态的联合概率,p(yt | xt-k)是给定 X 在时间 t-k 的状态时 Y 在时间t的状态的条件概率,而p(yt) 是在时间的状态的边缘概率。
转移熵的值越大,说明X对于Y的因果性更显著。与Granger因果关系不同的是,转移熵是针对非线性因果关系的有向刻画,可以捕捉更复杂的动态关系,同时两组序列的异向转移熵可能不同,这允许我们确定信息流动的方向。考虑到转移熵的计算特点以及日内信息的高阶相关性(详见《时序信息中的Alpha》)。因此,我们类比于之前的LBQ因子刻画方式,采用多期滞后项的方式计算量价层面的转移熵,进而刻画出量价的全局非线性因果性。最终,我们将基于转移熵序列计算其均值:均值越大说明对应的风险相应越小,预期收益越高,为正向因子。之后我们在时序上取20日均值作为因子,分为叫做te_v2r与te_r2v。
3.3因子表现
从日度IC测试结果上看,量价非线性因果因子表现较好,其中收益率→成交量方向刻画的因子更为出色,Rank IC均值为0.045,ICIR大于0.5,表现出较好的股价预测能力。

从日度组合测试结果上看,量价非线性因果因子的表现十分优秀,多空夏普均较高,且无明显回撤,多头收益率较高,收益率→成交量的因子表现更优。具体来看,从多空组合测试上看,te_r2v的多空收益率在47%左右,多头收益率约为17%,夏普比率在5左右。

从Rank IC时序特征、多空净值曲线以及分位数组合测试结果上看,te_r2v因子的多空净值长期呈现上升趋势,且无明显回撤,表现十分稳定
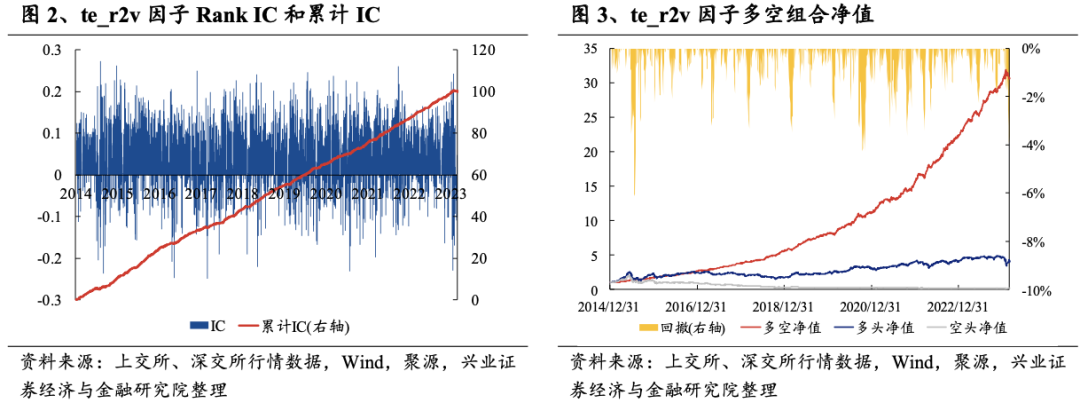
3.4因子相关性检验和正交化处理
由于两者在逻辑和相关性上接近,我们最终将两者等权合成得到te_Comb因子,并将其与时序相关性最高的已有高频因子进行正交化处理,得到te_CombN因子。经过正交化后该因子与底层所有高频因子的时序相关性均值约为26%,截面相关性均值约为17%,表现出较高的特异性。从日度IC测试结果上看,te_Comb因子表现较好,正交化前Rank IC均值为0.046,正交化后均值为0.025,ICIR分别约为0.5和0.4,表现出较好的股价预测能力。

从日度组合测试结果上看,te_Comb因子的表现十分优秀,多空夏普均较高,且无明显回撤,多头收益率较高,多空收益率在49%左右,多头收益率约为18%,夏普比率在5左右。经过正交化之后,其表现并未出现明显下降

4、关联信息中的局部特征:“交易时间”和持续期特征
在前序章节中,我们从关联信息的全局角度出发,构建了量价非线性因果关系因子,该因子也侧面论证了日内量价的关联信息存在着丰富的Alpha信息。在本章中,我们将进一步探究关联信息中的局部特征,从“自然时间”到“交易时间”,再进一步衍生出最终的个股的持续期特征。
4.1“自然时间”和“交易时间”
无论是日内还是日间,收益率的分布特征往往存在着明显的“尖峰厚尾”的现象。针对此现象,学术界和投资界均进行了诸多探索,并由此衍生出了丰富的研究内容。此前,大多数研究在讨论收益率特征时往往将“自然时间”默认为收益率的时序标签,如每个交易日收盘价的变动幅度等。在1973年,Clark首次在价格变动的随机过程中引入从属过程,将价格变动从“自然时间”变化至交易活动强度加权下的“交易时间”,进而更好地表示波动率聚集现象以及收益率的“尖峰厚尾”特征。从此之后,研究人员投入了大量的时间和精力来研究收益波动性与交易活跃度(如交易量和交易次数)之间的关系。
近年来,随着日内交易数据的逐步完善,学术界针对日内收益率的分布特征提出了同样类似的观点:“尖峰厚尾”是由于流动性资产在日内不同交易时间内的交易活跃度不同导致。在分钟或更高频的观测维度之下,每一个等量的时间间隔对于价格的影响作用并不相同。以同样两个分钟而言,成交量、成交金额和交易次数的不同将导致不同分钟对于价格的影响程度不同,进而导致价格出现自然时间上的“跳价”或变动较小。这本质上是“自然时间”和“交易程度”的不对等特征导致的。
4.2“交易时间”的刻画方式
参考Clark等相关研究的思路,在本节中我们将以成交量作为交易活跃度的刻画指标,尝试将“自然时间”调整为“交易时间”,致力于在相对统一的“交易时间”内衡量“量”和“价”的变动特征,进而挖掘出日内Alpha信息。具体来说,我们首先根据分钟级成交量和收盘价数据,刻画出统一的交易活跃度加权下的收盘价,即“交易时间”间隔下的收盘价数据。具体流程如下:
1. 设置“交易时间”阈值:类比于“自然时间”中60秒等于1分钟的设置,我们首先需要设定一个“交易时间间隔”的阈值。我们计算一只股票T日内分钟成交量总和,再进一步除以50得到成交量阈值 tradingVol ;
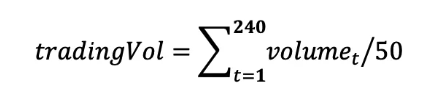
其中,volumet是第t个自然时间下的成交量。
2. 计算“交易时间”价格:进一步基于“交易时间间隔”计算活跃度加权下的收盘价。从第一分钟开始,我们逐步累加成交量,若成交量累加值达到“交易时间间隔”时,说明当前“交易时间”达到“一个时刻”。此时,我们将囊括在内的所有分钟收盘价按照分钟成交量占比加和,得到“交易时间”的收盘价;
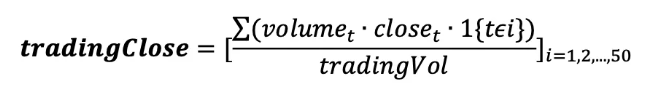
其中,tradingClosei 为第i个“交易时间”下的收盘价,volumet, closet 分别是第t个自然时间下的成交量和收盘价,1{k∊i} 表示当前自然时间k是否属于第i个交易时间。除收盘价,我们进一步统计每个“交易时间”的分钟间隔数,记为 tradingTime。
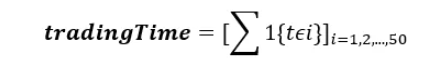
至此,我们根据每支股票每天的交易情况,将日内“自然时间”对应的数据刻画为“交易时间”,共计50个。其中,我们总共得到两组数据,一组代表每个交易时间的股价,另一组相当于“交易时间”与“自然时间”的转换关系。
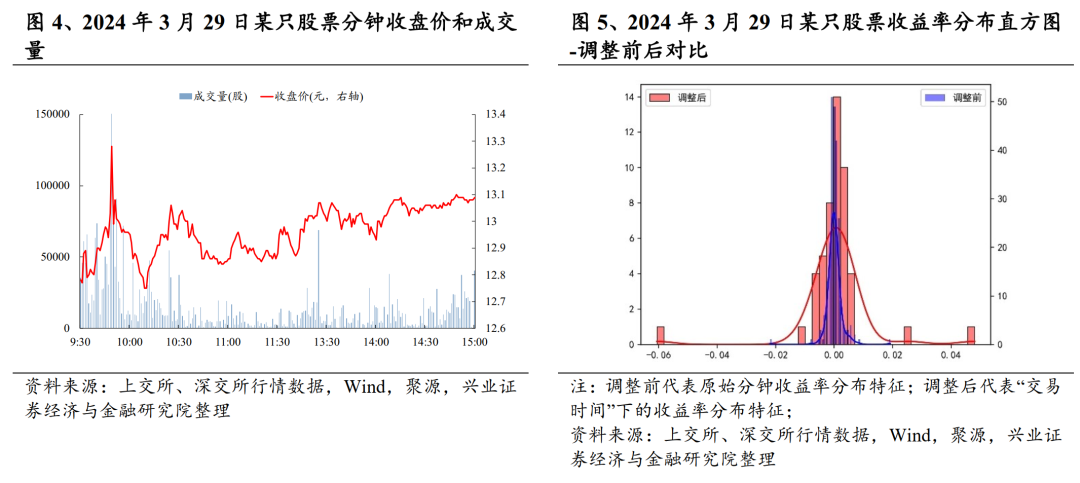
在上文中我们提及,转换为“交易时间”的目的之一是以交易活跃度作为衡量方式的情况下,收益率的“尖峰厚尾”特征会有所改变,分布将更加接近正态分布。我们以2024年3月29日某只股票作为样例,简单展示转换前后的股价特征和收益率分布。下图左侧展示了该股当日的收盘价和成交量,可以明显看出:该股在9点38分至9点50分左右出现过一次较大幅度的波动,价格由此前的12.8上涨至最高13.28,随后又下跌至12.75左右;下午该股整体走势相对平缓。从原始收益率分布特征上看(右侧图蓝色部分),该股呈现出相对明显的“尖峰厚尾”特征,其分钟收益率的峰度值为26.78,偏度值为-1.26,“尖峰”特征十分明显。之后我们通过上述算法将“自然时间”切换为“交易时间”后,其收益率分布的正态性得到了十分明显的改善,峰度值为16.94,偏度值为-0.53。从频率分布直方图和核密度图上看,调整后的分布(右侧图中红色部分)的正态性相对于蓝色也得到了明显的改善。这一对比说明:经过“交易时间”转换后的确部分了改善收益率分布的正态性。
4.3“交易时间”下的基础性因子表现与分析
经过上述的计算,我们已经可以基于每支股票当日的交易特征,刻画出“交易时间”下的股价走势以及每个“交易时刻”的时间间隔。在本节中,我们先尝试基于上述刻画出的两组数据构建因子。事实上,除了转化过程之外,本质上新的股价时序的数据特征和原始股价特征一致。我们首先统计“交易时间”下的收益率的均值和方差,作为“交易时间”下的收益率均值因子和已实现方差因子,记为cutVol_rtnMean和cutVol_rtnVar。此外,我们进一步统计“交易时刻”的时间间隔序列的均值和方差,作为“交易时间”下的时间特征均值因子和方差因子记为cutVol_timeMean和cutVol_timeVar。
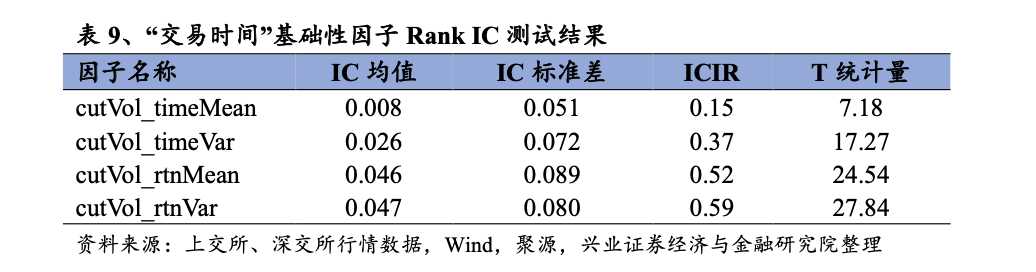
从日度IC测试结果上看,除单个因子之外,“交易时间”下的基础性因子表现较好,其中cutVol_rtnMean和cutVol_rtnVar因子更为出色:以cutVol_rtnVar为例,该因子的Rank IC均值为0.047,ICIR为0.59,表现出较好的股价预测能力。
从日度组合测试结果上看,“交易时间”下的基础性因子的表现十分优秀,多空夏普均较高,且无明显回撤,多头收益率较高。具体来看,从多空组合测试上看,cutVol_rtnMean的多空收益率在43%左右,多头收益率约为16%,夏普比率在5左右。
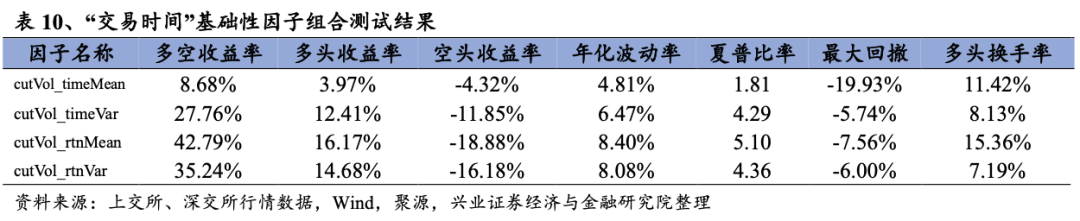
与之前的收益率均值因子和已实现方差因子类似,这类因子都是通过多个角度刻画收益率分布特征偏离正态分布的距离,也就是通过对异常交易行为的刻画来提取Alpha信息。但“交易时间”的刻画方面,我们在加入交易活跃度作为从属特征,从一定程度上避免了诸如流动性、集中交易导致的收益率偏移。换个角度而言,如果在“交易时间”下收益率仍然明显偏移正态分布,其异常交易行为的特征将更加明显,由此得到的Alpha信息也应当更加纯粹。因此,理论上cutVol_rtnMean和cutVol_rtnVar应当能够包含不同于普通日内收益率均值和方差因子。从时序相关性的检验上看,这两个因子对应的相关性最高的因子正是均值和方差因子。我们将其分别进行正交化之后,两个因子与底层所有高频因子的相关性均值分别约是23%和20%。
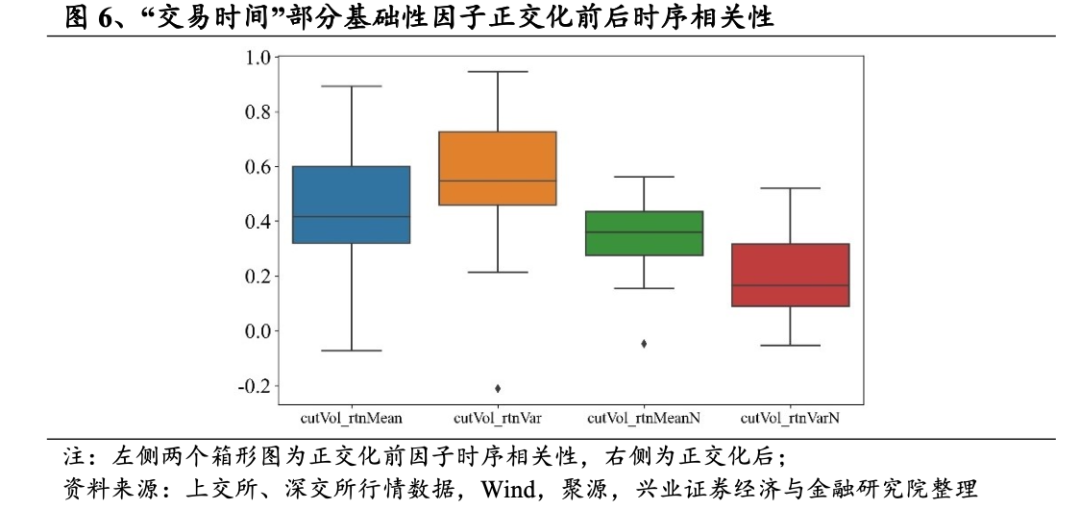
我们进一步展示两个因子正交化之后的回测结果,具体如下。从日度IC测试结果上看,正交化之后“交易时间”下的基础性因子表现同样优秀,两个因子的Rank IC均值在0.023左右,ICIR仍然在0.50左右,表现出较好的股价预测能力以及特异性。
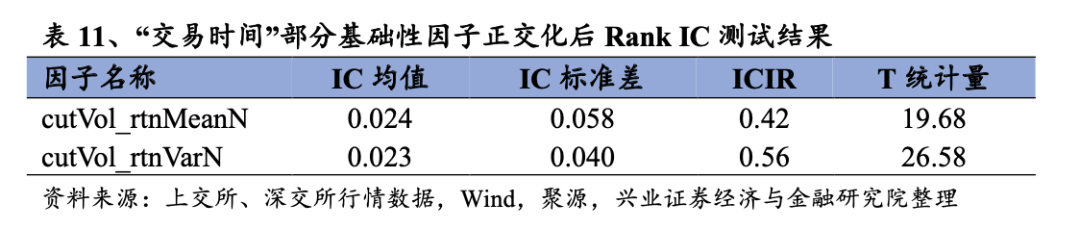
从日度组合测试结果上看,“交易时间”下的基础性因子的表现十分优秀,多空夏普均较高,且无明显回撤,多头收益率较高。具体来看,从多空组合测试上看,cutVol_rtnVarN的多空收益率在22%左右,多头收益率约为13%,夏普比率在5.5左右,表现出较好的稳定性和特异性。

从多空净值曲线以及分位数组合测试结果上看,两个因子的多空净值长期呈现上升趋势,且最近几年无明显回撤,表现十分稳定。
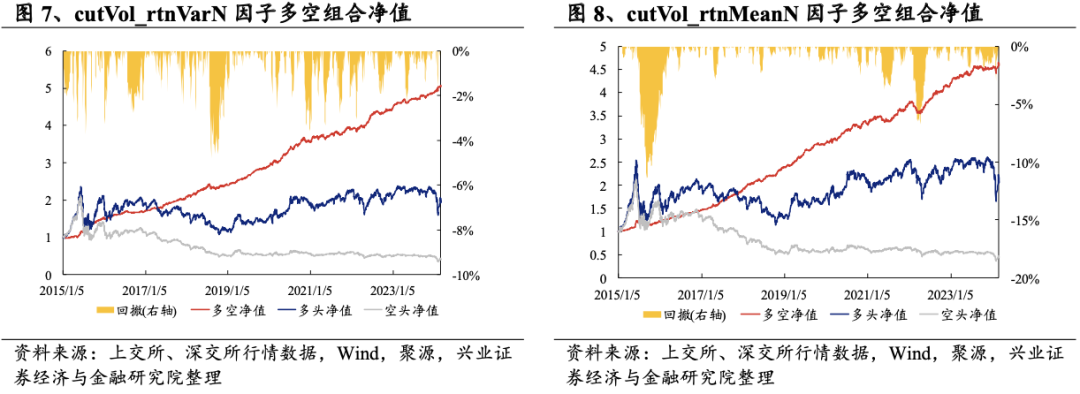
综上,“交易时间”的转化本质上是在统计个股日内异常特征的同时,通过标准化交易量的方式避免诸如流动性、集中交易导致的收益率异常值,进而提取相对更加纯粹的日内信息。从上述结果上看,即便是同样的统计量,“交易时间”和“自然时间”下构造的因子也存在明显的差异性,能够以此构造出更加丰富的高频因子。
4.4“交易时间”与交易聚集性
在上文中,我们基于成交量将“自然时间”转换为“交易时间”,并重点集中于转换之后价格信息,刻画了分布特征因子,表现出较好的选股能力和特异性。上文的高频因子相对于偏向基础的统计。在本章中,我们尝试进一步深耕“交易时间”带来的增量信息—分钟统计下的条件持续期模型。
在现有的日内Level-1数据研究中,高频数据均是在细小的时间间隔上抽取的观测值,并将原始数据过滤产生新的固定频率的数据,例如对频率更高的逐笔成交数据通过切片的方式将数据调整至分钟频率上。这种处理方法能够高效地清理出体量更小、更适合直接应用的高质量高频数据,但同样也降低了数据频率,并丧失交易数据的某些特性,其中便包括了交易发生的间隔时间。在上文中,我们已经通过自行设计的算法刻画出了“交易时间”,每一个“交易时刻”时序数据代表着一个单位交易量下的时间间隔和股价变动。那么,我们能不能通过“交易时间”下的数据,刻画出交易发生的间隔时间呢?事实上,我们可以将“交易时间”视为一个简单的点过程:考虑 ti是第 i 个“交易时间”到达时对应的“自然时间”,从第 i-1 到第 i 个“交易时刻”的时间间隔为∆ti = ti - ti-1。对于上述刻画出的50个日内“交易时刻”而言,我们同样可以得到50个间隔时间,记为交易到达的间隔时间,每一个间隔时间代表着下一笔同等交易水平的到达时间。
与股价的时序模型类似,交易到达的间隔时间也存在着部分异常特征,其中最为著名的便是交易的聚集性。交易聚集性类似于波动率聚集现象:较短的交易间隔时间后面也往往跟随着短的交易间隔时间,长的交易间隔时间后面也往往跟随着长的交易间隔时间。举例来说,A股市场的成交量分布呈现出十分明显的“U型”分布特征:即开盘和收盘阶段的交易强度较大,如下方左图。这便是交易聚集性的典型体现。此外,股票市场存在着大量的“跟风交易者”,这导致部分时间点成交量出现激增。如下方右图中,我们计算该股日内五分钟滚动成交量之和。可以明显看出,该股日内的成交量呈现出十分明显的聚集现象:部分时间段成交量集中增加。
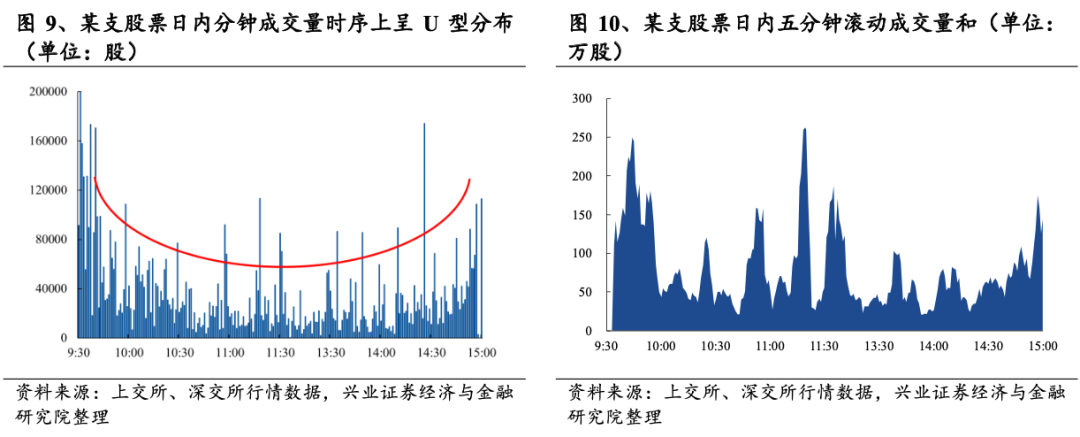
针对上述特征,学术界引入持续期模型,以便在考虑交易聚集性的情况下构建交易间隔时间的时序模型,其中一个便是ACD(Autoregressive Conditional Duration)模型。ACD模型与GARCH模型类似:GARCH模型是刻画波动率的聚类性,ACD模型是刻画交易的聚类性。具体来说,通过考虑交易活动的随机性和时间间隔的非等间隔性,ACD模型旨在更准确地描述金融市场的微观结构,并预测交易发生的时机。通常来说,ACD模型采用极大似然估计法估计模型中的参数,进而根据样本数据刻画中交易间隔的聚集性现象的强度。然而,此类模型的计算复杂度相对较高,同时并未将股价涨跌特征纳入考虑:更大的涨跌幅度是否会影响间隔时间。本节中,我们将从两个角度出发,参考ACD模型的假设刻画出日内股票的聚集现象。
- 检验方式1:时序相关系数
对于一个时间序列而言,时序相关系数是检验聚集性最为有效且最简单的方式之一。我们基于“交易时间”的时间间隔数据(共计50个),统计间隔数据的一阶自相关性,记为cutVol_timeCor因子。自相关性越大,说明时序上时间间隔存在着相对明显地聚集性。
- 检验方式2:分桶熵
在上述统计方式中,我们仅考虑了交易时间自身,并未引入股价涨跌特征。在本节中,我们在引入股价涨跌特征的同时,参考之前《高频研究系列四—成交量分布中的Alpha》的方法,从整体性的角度出发刻画交易时间的分化特征,进而反向刻画出交易聚集性的强度。
分桶熵的思路类比于我们在报告《高频研究系列四—成交量分布中的Alpha》中的思路,本质上是刻画一组数据的分化程度与随机性:如果同号同大小的时间间隔数据大量出现,如大量出现上涨且间隔绝对值均为3的数据,说明该股出现了交易聚集现象,整体交易规则呈现出极强的一致性,反之我们可以认为交易的时间间隔相对随机。综上,上述两个因子均为正向逻辑的因子,即因子值越大,股票的交易聚集现象更加强烈。最终我们计算过去20个交易日的均值,作为最终的因子值进行测试。
从日度IC测试结果上看,交易聚集性相关因子表现较好,其中cutVol_timeCor因子更为出色,Rank IC均值为0.045,ICIR约为0.5,表现出较好的股价预测能力。

从日度组合测试结果上看,交易聚集性相关因子的表现也十分优秀,多空夏普均较高,且无明显回撤,多头收益率较高。从多空组合的夏普比率上看,cutVol_entropy的表现更为优秀,其多空收益率在24%左右,多头收益率约为11%,夏普比率在4左右。

从Rank IC时序特征、多空净值曲线以及分位数组合测试结果上看,cutVol_entropy因子的多空净值长期呈现上升趋势,且最近几年无明显回撤,表现十分稳定。
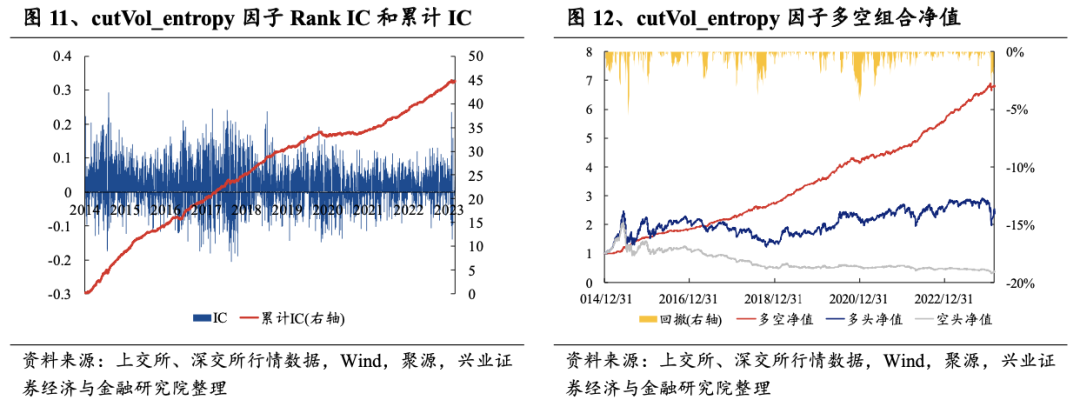
4.5因子相关性检验和正交化处理
我们进一步进行时序和截面相关性检验。其中,cutVol_entropy表现出极强的特异性,其与底层所有高频因子的时序相关性低于35%,均值仅16%。对于cutVol_timeCor,我们将其与时序相关性最高的已有高频因子进行正交化处理,得到cutVol_timeCorN因子。经过正交化之后,该因子与底层所有高频因子的时序相关性均值约为35%。从日度IC测试结果上看,cutVol_timeCorN因子表现较好,正交化后Rank IC均值为0.022,ICIR约为0.4,表现出较好的股价预测能力。

从日度组合测试结果上看,cutVol_timeCorN因子的表现同样优秀,多空夏普均较高,且无明显回撤,多头收益率较高,多空收益率在16%左右,多头收益率约为8%,夏普比率在3左右。

5、关联信息中的典型特征:再论“闪电崩盘”
在前序章节中,我们从关联信息的全局角度和局部特征出发,构建了量价非线性因果关系和“交易时间”相关因子。在本章中,我们将角度进一步缩小,从某一具体的量价特征出发,构建带入量价信息的“V型”走势特征与最终的改进后“闪电崩盘”因子。
5.1“闪电崩盘”因子回顾与反思
在往期报告《高频研究系列六—时序信息中的Alpha》中,我们首次提出“闪电崩盘”这一概念。具体来说,我们将“闪电崩盘”通指为流动性资产的价格在日内短时间出现大幅超跌,同时后续允许价格出现恢复,即在日内出现深“V”的价格走势,如下图所示。
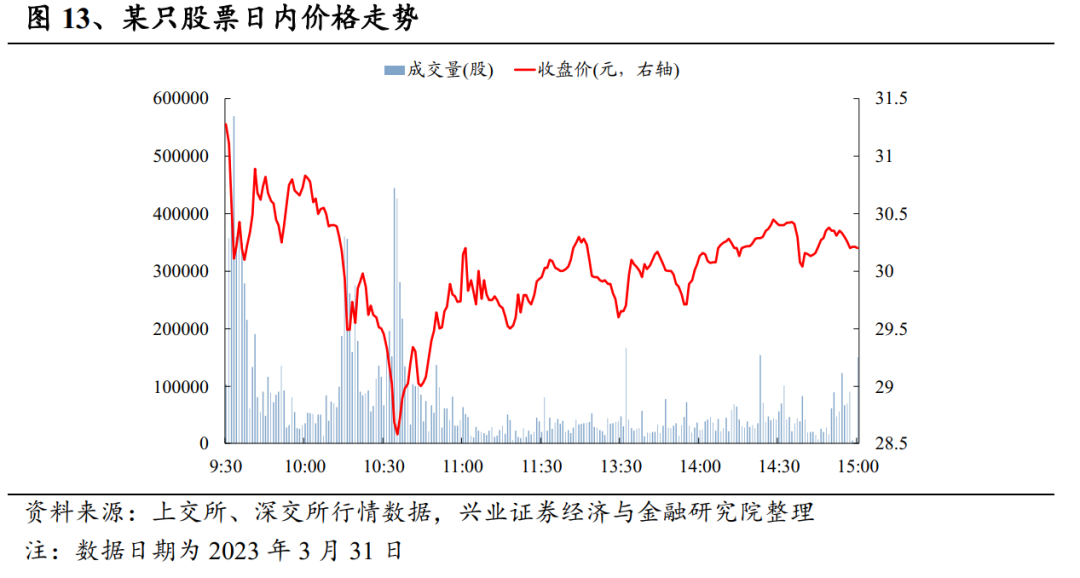
在前序的研究中,我们以连续下跌次数作为出发点,通过刻画日内分钟级收益率连续下跌次数序列引出“快速下跌”这一特征,并进一步引入泊松分布,以表示未来一段时间内,能够出现“快速下跌”的概率,进而构建“闪电崩盘”flashCrashProb因子。无论是在截面选股层面还是时序层面,该因子均表现出了较好的预测能力,并能够基于概率表达动态剔除预期可能会下跌的股票。具体算法可参考发布于2023年6月29日的报告《高频研究系列六—时序信息中的Alpha》。截至2024年3月底,该因子已在样本外跟踪近1年。从回测全时段上看,该因子Rank IC均值为0.014,多空夏普比率为2.68。


从Rank IC时序特征、多空净值曲线以及分位数组合测试结果上看,flashCrashProb因子的多空净值长期呈现上升趋势,且最近几年无明显回撤,尤其是2024年初并无明显回撤,表现十分稳定。
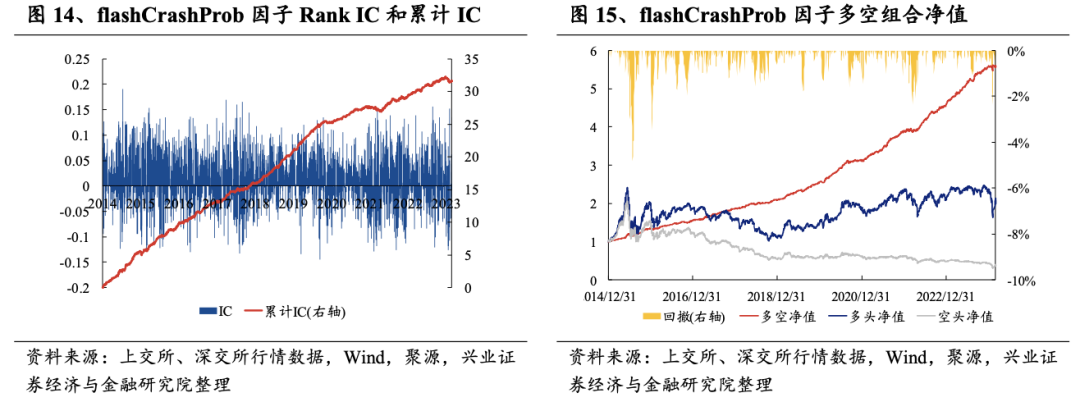
在往期的研究中,我们在刻画“快速下跌”特征时仅单一地考虑了下跌的分钟累加数,也就是时间间隔的概念。从本质上说,日内股价的下跌特征能够从多个方面进行刻画,包括下跌幅度、下跌中放量情况等。此外,将一次下跌和一次上涨合并刻画也更加符合“V型”特征。如下图样例所示,左侧两个收益率序列在下跌次数计算中均为连续10次下跌(10点至10点10分),但从幅度上看,蓝线的下跌幅度更大。在后续走势中,两者呈现出不同的走势:蓝线在下跌后出现一定幅度的上涨,红线则相对震荡,最终价格相对接近。在现有的统计中,两者在连续下跌和连续上涨次数统计中结果相对一致,但显然蓝线走势更加符合“V型”下跌的特征。此外,除收盘价序列之外,蓝线在下跌过程的放量特征更加明显(下方右图)。因此,现有的全局次数统计法难以精准地刻画出类似于“V型走势”这样的典型特征。
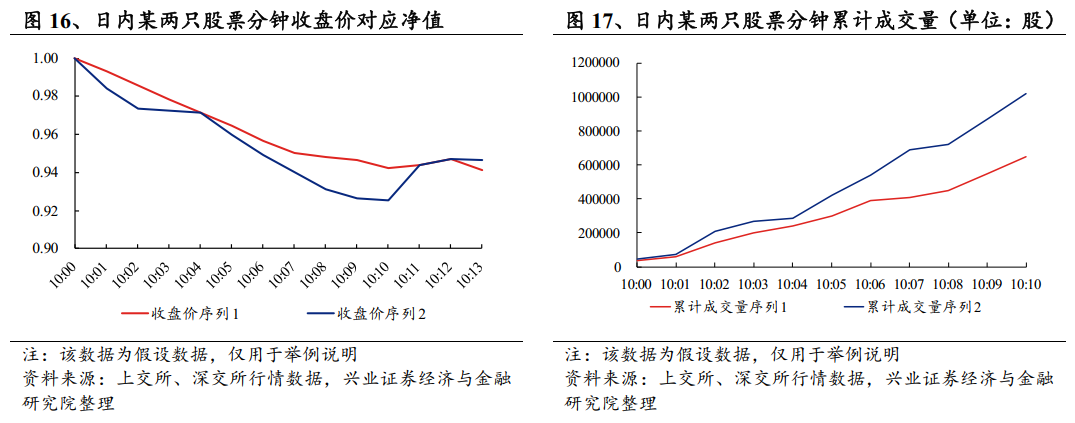
综上,尽管该因子在样本外仍保持了一定的预测能力,但其刻画的事件相对宽泛,且对于“V型”这一典型特征的刻画精准度相对一般,且并未考虑除下跌次数以外的额外信息。因此,我们将在此前的研究基础之上,对该因子进行改进。具体来说,我们将改进分为两个步骤:第一步我们将基于量、价和时间三维度的信息,刻画股票的“V型特征”;第二步我们将基于“V型特征”,刻画新的“闪电崩盘”概率因子,并衡量其有效性。
5.2改进步骤1:“V型特征”的刻画
前文提及,日内股价的“V型特征”可能包含三维度的信息:股价走势的幅度、持续时间和成交量特征。沿用此前的想法,我们在此前的基础之上,我们加入幅度、成交量和间隔时间等多个维度的信息,刻画股票日内“V型特征”,具体算法如下。
1. 计算分钟量价幅度序列:在每一分钟,首先计算分钟级对数收益率和分钟级成交量占比数据,相乘得到分钟量价幅度数据序列 rv :
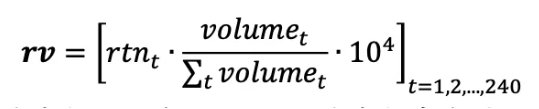
其中, rtnt 为分钟收益率,volumet 为分钟成交量,rv 代表着考虑了量价共同作用的股票走势,记为量价幅度。更大的成交量、更大的振幅将会得到更大的量价幅度。
2. 计算累计分钟量价幅度序列:沿用之前报告的想法,我们同样计算同号累加值,但此时是针对量价幅度序列进行累加:若一个量价幅度为负数,则开始统计连续量价幅度为负数之和,直至下一个量价幅度非负,则停止计数,该个数则为一个累计量价幅度样本点;
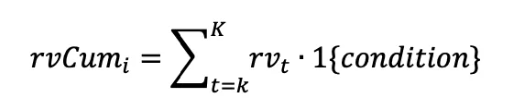
其中, condition 表明前序累加的量价幅度同号。最终我们由此得到多个连续下跌量价幅度样本点,该数据应当为正负号相接的一组序列。
3. 刻画“V型”特征:在“V型”特征中,股价应该为大幅度下跌,小幅度上涨,且下跌幅度大于上涨幅度的一段走势。根据之前得到的累计量价幅度,我们按要求计算 为负数、为正数的两者之和,并筛选和为负数的数据,取绝对值作为最终的“V型”走势特征 r𝒗V。
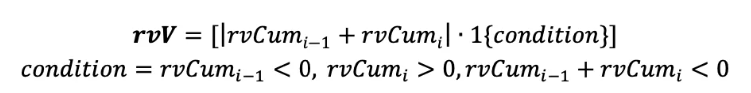
除此之外,我们还可以得到每个“V型”走势的持续分钟数,记为 timeV。
综上,在每日收盘后,我们根据股票自身的日内走势,将收盘价、成交量和时序特征三者进行综合考虑,并在最终刻画时同时考虑下跌和上涨的连续性,最终得到每只股票日内的“V型”走势特征。我们以上文中提及的样例进行展示计算,并表示如下。在此前的样例中,两只股票前10分钟均下跌,在原先的计算中得到连续下跌次数均为10,不存在差异。在目前的计算中,我们首先根据价格振幅和成交量占比计算出量价幅度,再累加得到10点10分的累计量价幅度,分别约为-11.2和23.9。在考虑了下跌幅度和交易情况之和,明显第2个序列的下跌特征更加明显,对应幅度累加值也同样更大。此后两者均上涨两分钟,得到累计幅度为2.5和4.9。之后两股均下跌,由此我们得到一个完整的“V型”走势。按照上诉算法,我们得到两只股票的“V型”走势特征分别是8.68和19.05,两者的“V型”走势持续分钟数均为12。显然,在目前的算法中,我们对于“V型”走势特征的刻画能够清晰地区分出下述两种股票的走势差异,进而找出“V型”走势特征更加明显的2号股票。
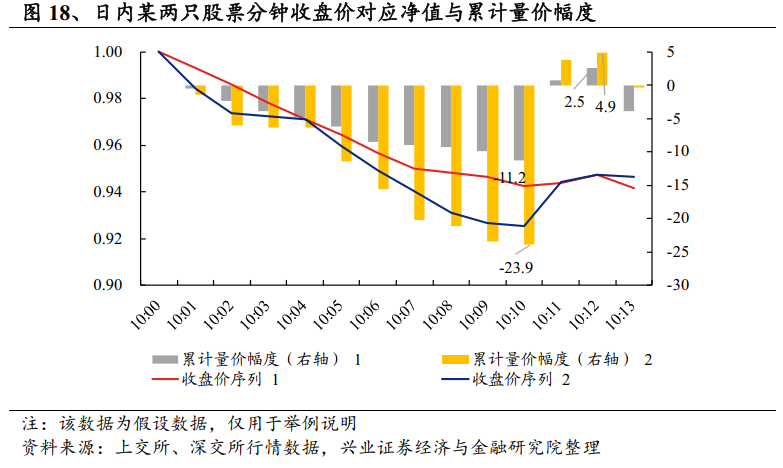
5.3改进步骤2:“V型”特征基础因子构造与表现展示
在上一章节中,我们基于价格、幅度和时间的三者信息,联合得到最终个股的“V型”走势幅度和时间数。在本节中,我们将首先基于得到的数据构建“V型”特征基础因子。
具体来说,我们根据每只股票的“V型”走势特征序列,计算均值和最大值,记为negV_mean和negV_max。均值或最大值越大,说明“V型”特征的走势越明显,股价日内风险较大,预期收益较低。此外,我们还可以将“V型”走势特征除以对应的持续分钟数,以刻画时间加权下的“V型”走势特征,持续时间越短且原始走势特征越大,“V型”走势特征越强烈,对应数值越大。我们同样计算时间加权下“V型”走势特征的均值和最小值,逻辑与上述一致,记为negVwgt_mean和negVwgt_max 。最终我们在日度时序上取过去20日均值,得到最终的因子值。
从日度IC测试结果上看,“V型”走势基础因子表现较好,其中原始“V型”走势特征的相关因子表现更为出色,最小值计算得到因子表现也更为出色,以negV_max为例,该因子Rank IC均值为0.031,ICIR约为0.5,表现出较好的股价预测能力。
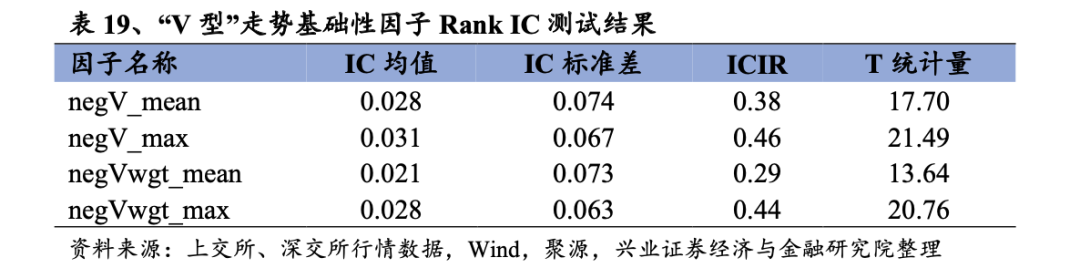
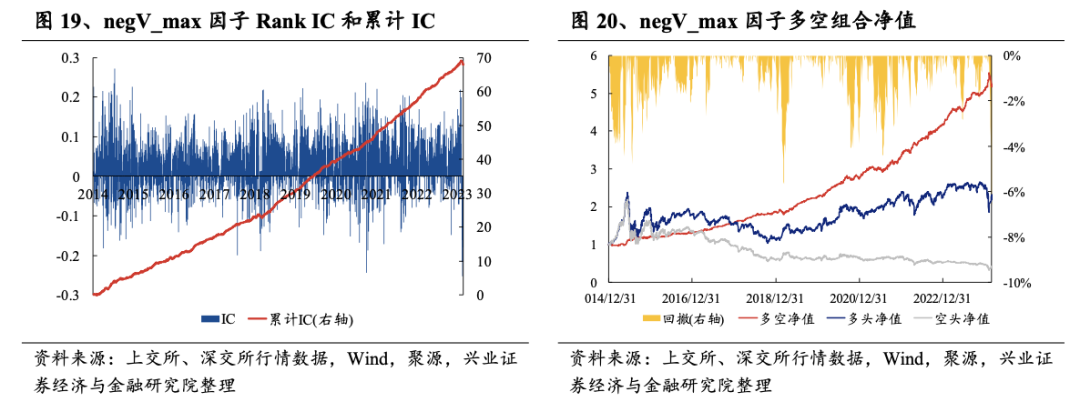
从日度组合测试结果上看,“V型”走势基础性相关因子的表现也十分优秀,多空夏普均较高,且无明显回撤,多头收益率较高。从多空组合的夏普比率上看,negV_max的表现更为优秀,其多空收益率在20%左右,多头收益率约为10%,夏普比率在3左右。

从Rank IC时序特征、多空净值曲线以及分位数组合测试结果上看,negV_max因子的多空净值长期呈现上升趋势,且无明显回撤,表现十分稳定。
5.4改进步骤3:“V型”特征下的“闪电崩盘”概率
至此,我们已经通过算法改进了日内股价走势典型特征的刻画,得到了每只股票的“V型”特征序列。在前序研究中,我们引入泊松分布刻画概率,并发现“闪电崩盘”概率有别于其他高频因子,其本身概率化的含义不仅能够在截面上对股票进行排序,同时还能在时序上刻画流动性资产的未来风险。在本章中,我们同样尝试将“V型”特征通过类似的想法进行概率化,进而得到最终的“闪电崩盘”概率因子。
在上述的计算中,我们发现:日内出现过“V型”特征的股票,其预期收益更低。然而,在现有的结果中,“V型”特征本身由此前的正整数值变为了实数值,并不满足泊松分布的实际含义和分布特征。在目前的情况,我们需要刻画的是:在未来一天内,发生“V型”走势特征数值小等于某一阈值的概率是多少。因此在本节中,我们将改变思路,使用更为贴切的连续性分布刻画“闪电崩盘”概率。该概率是在表达:对于某一只股票而言,最为明显的“V型”走势特征能够超过全市场前25%的概率为多少,数值越大则说明未来发生“闪电崩盘”的概率越大。
5.5改进步骤4:“闪电崩盘”概率应用
在计算因子值之前,我们首先根据闪电崩盘概率,统计其对于预期风险的规避能力如何,也就是:如果当期某些股票的“闪电崩盘”概率较高,其未来短期内是否会出现相对明显的负向收益。
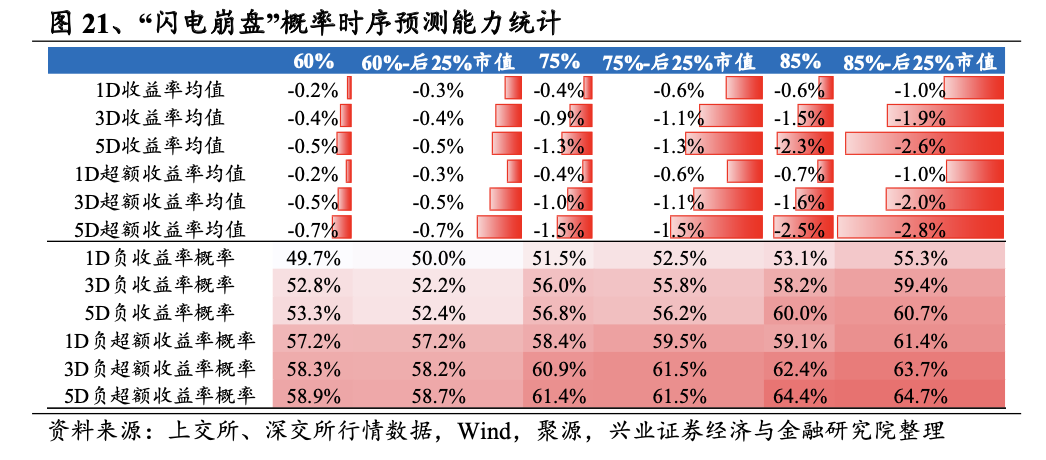
在测算层面。我们设置发出警示信号的阈值分别是60%、75%和85%,即概率超过阈值时,该股被给予警示信号,我们统计其未来1日、3日和5日的区间收益率和区间超额收益率,并进一步统计时序上所有被给予警示信号的股票的收益率均值、超额收益率均值以及负向收益率样本数占比。此外,由于小市值股票的“崩盘”概率从逻辑层面上概率较高,我们进一步以流通市值25%分位点作为范围,单独统计对应阈值下对小市值股票的预测能力。统计结果展示如下。
我们的测试时间区间和全文设置的回测区间一致,且为每日判断。从测试结果上看,所有测试维度中的收益率和超额收益率均值均为负数,且负向收益率概率基本在55%以上,这说明“闪电崩盘”概率在时序上具备一定的风险预测能力。以75%作为阈值统计,未来3或5日的负向收益率概率约为56%,在小市值中统计得到的结果也类似;此外,未来3或5日的负向超额概率达到约60%,在小市值中也类似,具备较强的预测能力。此外,随着阈值的逐步提升,指标的预测能力逐步提升,呈现出明显的单调性。
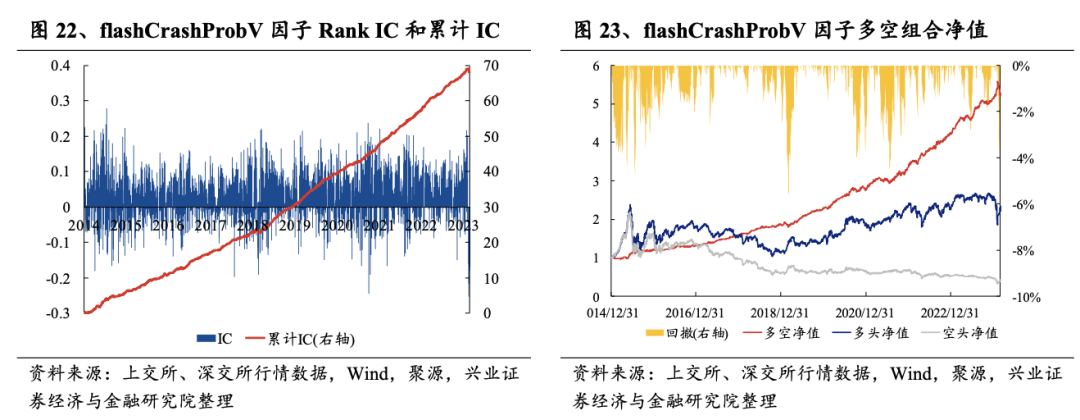
上文展示了“崩盘”概率在时序上的规避风险能力。进一步,我们在日度层面取过去20日均值,作为最终的“V型”特征下的“闪电崩盘”概率因子,记为flashCrashProbV。从日度IC测试结果上看,该因子表现较好,Rank IC均值为0.031(同期此前闪电崩盘因子均值为0.014),ICIR约为0.5,表现出较好的股价预测能力。

从日度组合测试结果上看,该因子的表现也十分优秀,多空夏普均较高,且无明显回撤,多空收益率在21%左右,多头收益率约为10%,夏普比率在3左右。

从Rank IC时序特征、多空净值曲线以及分位数组合测试结果上看,flashCrashProbV因子的多空净值长期呈现上升趋势。
6、总结
本文中,我们基于日内的“量、价、时”三维度信息,由浅入深地刻画日内的关联特征,并基于该维度信息构建了三大类新因子。整体来看,构造出的新因子表现优秀,同时具有优秀的特异性。我们将继续深耕该方向,继续为投资者提供更加新颖丰富的研究。
附录 回测说明
在本文中如无额外说明,我们因子的回测规则设定如下:
- 因子回测区间:2014年12月31日—2024年3月31日;
- 回测规则:剔除当期不在市、涨跌停以及特殊处理的股票;
- 交易规则:对于T日收盘构建的因子值,我们首先于T+1日判断当日股票的交易情况,剔除当日不可交易和涨跌停的股票后于T+1日买入,并于T+2日卖出;
- 回测结果说明:本文中,回测表格中提及的年化波动率、夏普比率、最大回撤、胜率均为因子回测时的多空净值对应统计量,多头换手率为多头组的单边换手率,且我们这里的多空是两分组并按照因子值进行加权(参见《高频漫谈》)。
风险提示:模型结果基于历史数据的测算,在市场环境转变时模型存在失效的风险。
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
