作者:嘟嘟的投研CheatSheet,好投学堂专栏作家
题图:嘟嘟的投研CheatSheet微信公众号
低相关可能是为数不多的“免费午餐”,之前在《基研CheatSheet · 组合投资是正道》已有过论述。
今天分享下我自己这一年来践行自研高波动复合策略产品的思考,也是我对半年前路演材料的一次迭代。
高波动组合涉及哪些底层策略?
首先,低波动子策略通常不在考虑范围内。因为即便是高波动子策略,搭配以后组合波动率也大幅下降;如再使用低波动子策略,将显著降低资金的利用效率。
在只考虑国内资产的前提下,包括主观股票、主观CTA、主观转债、量化股票、量化CTA、量化转债、宏观对冲、商品指增等,都是高波动组合构建过程中可选的策略大类
进一步展开,像主观股票涵盖了核心资产、价值红利、科技成长、均衡等不同风格小类,量化CTA包含时序和截面两种小类,量化股票也涉及300、500、1000、空气指增等小类。
大类小类策略如何取舍?
一方面,取决于组合主理人的认知跟能力边界。果断放弃自己不擅长的领域,比如我放弃了主观CTA、主观转债、宏观对冲以及商品指增这几个大类策略,放弃的原因如下:
主观CTA:详见《基研CheatSheet · 主观权益和主观CTA的南辕北辙》,主要考虑无法自研、无MOM实操空间、无产业背景、对交易不敏感等。
主观转债:转债对应正股多为小公司,本身就不具备太大的主观分析空间,主观基金经理鲜有能在中证800以外样本大量持股的案例。
宏观对冲:不认可择时的方法论,统计上不支持,业界鲜有成功案例。
商品指增:详见《基研CheatSheet · 商品指增价值几何?》,不能因为这几年商品指数Beta很强就盲目冲,2011到2015年的熊市不能忽视。
另一方面,取决于小类策略之间的低相关性。
因为我自己有主观多头的自研策略,该策略选股域集中在中证800成分股,因此在规划量化策略时,会考虑尽量不触碰中证800的范畴,从而实现更好的对冲效果,因此搭配的是自研量化转债和自研量化小市值。
其中,没有选择常规的500和1000指增,是因为量化转债跟500指增、1000指增有极高的相关系数,且量化转债有比500和1000指增更优的收益风险比。
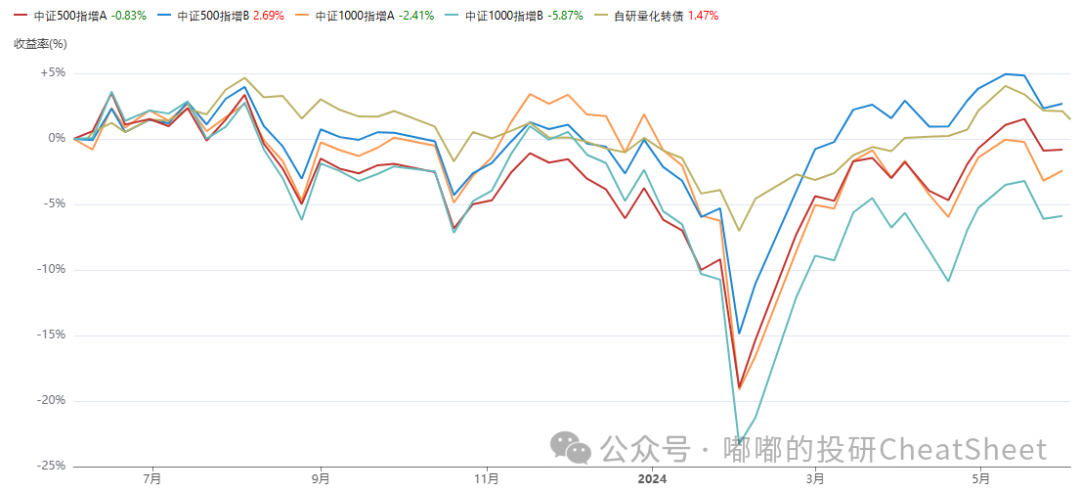
注:指增A、B分别来自两家口碑优良的百亿大厂
图表 量化转债与指增相关系数(非超额)
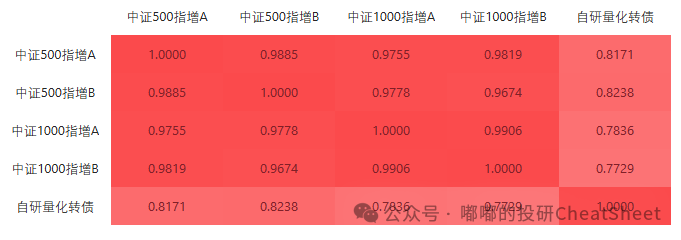
而在量化小市值情绪很差的当下,我依然建议维持一定的配置比例,因为即便在退市制度完善的美国市场,小市值板块也并没有出现持续走弱的Beta。
图表 美股“微盘” VS 美股“2000” VS 美股“500”
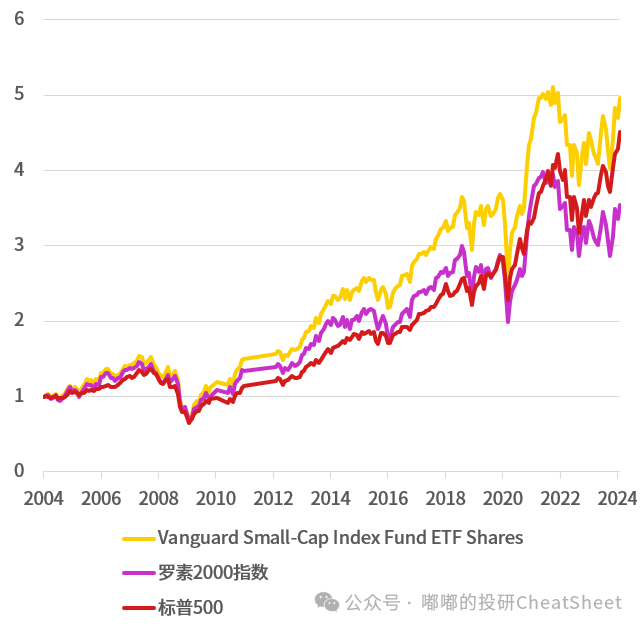
注1:罗素2000是罗素3000中市值最小的2000家公司,罗素3000是美股市值最大的3000家公司。由于美股目前有5000多家上市公司,所以罗素2000的地位大致介于国内的中证1000和中证2000之间。
注2:Vanguard Small-Cap是复制CRSP US Small Cap Index的ETF,该指数是根据流通市值从大到小排序,选取流通市值排名靠后的20%的股票,地位类似于国内的微盘股。
注3:长期看,美股的“微盘”跟美股核心资产标普500“不分伯仲”。
当量化转债跟微盘、主观多头进行搭配时,两两相关系数可以控制在较低水平。
图表 量化转债与主多、微盘相关系数(非超额)
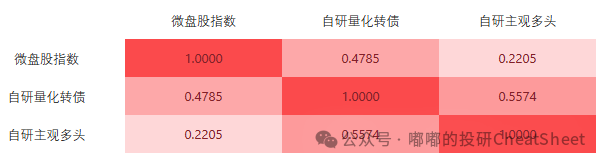
最后留在我高波动复合策略组合中的策略类型包括:主观均衡多头、量化偏股转债、量化小市值、量化趋势CTA。
这几类策略的底层收益来源也有较大区别,像主观多头的收益主要来自持有,跟宏观经济周期有更高的相关性;而量化转债跟量化小市值的收益不少来自于反转交易,像转债隐含的期权价值更是提供了差异化的盈利来源;而趋势CTA则是典型的追涨杀跌,与前面三者呈现零相关甚至负相关。
几类子策略如何分配仓位?
首先,明确组合的优化目标,主要分为:最小化波动率、最小化下行风险(只考虑下行波动率)、均值方差(最大化夏普)、最大化预期收益、风险平价等。
考虑到我的组合定位是让投资人有更好的持有体验,因此均值方差(最大化夏普)原本是不二之选,不过该优化目标对子策略收益率的假设过于敏感(大家可以拿代码测试下不同的数值),因此最终选择了风险平价作为优化方向。
其次,假设子策略的参数,风险平价主要涉及年化波动率和相关系数矩阵。这两部分的参数大家可以按照自己对策略的理解来填写,我使用了3个月产品的真实数据平滑处理。
# 子策略年化波动率:主观多头、量化转债、量化小市值、量化CTA
volatility = np.array([14, 9, 19, 22]) / 100
# 相关系数矩阵
correlation_matrix = np.array([
[1, 0.55, 0.22, -0.05],
[0.55, 1, 0.48, -0.27],
[0.22, 0.48, 1, -0.26],
[-0.05, -0.27, -0.26, 1]
])
# 协方差矩阵
cov_matrix = np.outer(volatility, volatility) * correlation_matrix紧接着使用minimize函数对目标函数进行优化,主要代码如下:
# 优化
opt_result = minimize(risk_parity_objective, init_weights, args=(cov_matrix,),
method='SLSQP', bounds=bounds, constraints=constraints)
# 计算每个资产的风险贡献
def risk_contributions(weights, cov_matrix):
portfolio_volatility = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights)))
marginal_contrib = np.dot(cov_matrix, weights) / portfolio_volatility
return weights * marginal_contrib
# 定义目标函数:最小化风险贡献之间的平方差
def risk_parity_objective(weights, cov_matrix):
contributions = risk_contributions(weights, cov_matrix)
return np.sum((contributions - np.mean(contributions)) ** 2)最后,得到四大策略的配置比例。以我自己的自研策略当前时点的配置为例,主观均衡多头理论应占22%、量化偏股转债占35%、量化小市值占20%、量化趋势CTA占23%。
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
