作者:量化君也
题图:量化君也微信公众号
在金融投资和量化交易领域,机器学习算法越来越受欢迎,也越来越普遍,因为咱人类一般通过观察能发现因果之间的线性关系,而非线性关系就不得劲儿了,于是乎,就要靠着这些机器学习算法帮助咱做出更明智的投资交易决策。
在这篇文章里面,咱唠唠在金融投资和量化交易当中,常用的并且效果还不赖的10大机器学习算法,会大概讲述其基本工作原理、用法用途和代码案例,主要是为量化萌新们起到“算法清单”的作用,文章篇幅有限,难以面面俱到,还望海涵~开整~~
一、线性回归(Linear regression)
线性回归应该可以说是最常用的一种统计模型了,高中就接触过的最小二乘法OLS就属于线性回归,你瞧,这也算是早期接触机器学习的案例了。
线性回归基于一个或多个自变量预测因变量的值,它之所以被称为“线性”,那是因为它假设因变量和自变量之间的关系是线性的,形式如y=a0+a1*x1+a2*x2+...+an*xn,其中x是自变量,y是因变量,a就是回归系数,a0又被称为截距。
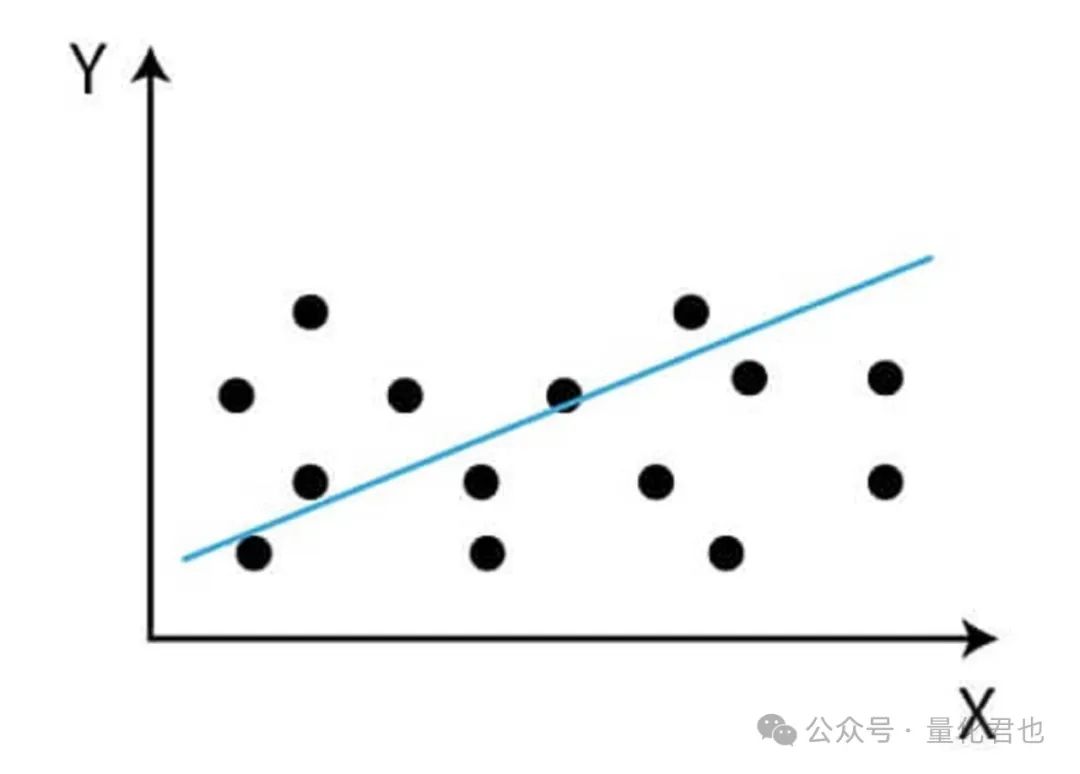
在金融投资和量化交易领域,线性回归经常被用来建模和预测金融时间序列/横截面数据,比如证券价格、因子收益、汇率和利率等等。它可以用来识别不同变量/因子之间的关系,并基于这些关系对未来值进行预测。
线性回归主打的优点就是其简单性和可解释性,不信你瞧,咱常见的资本资产定价模型(CAPM)、套利定价模型(APT)和Fama-French三因子等等模型都是表达成这种形式。
线性回归模型除了应用广泛之外,还非常容易实现,即使在大数据集上,它的训练速度也相对较快,并且还可以通过使用虚拟变量来处理缺失数据和分类变量。
现在使用这些机器学习算法已经非常方便了,都是封装好的库(例如scikit-learn),直接调用就可以了,下面来看看线性回归的实例源码。
import numpy as np
from sklearn.linear_model import LinearRegression
# 构建数据样本
X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
y = np.array([1, 2, 3, 4])
# 创建线性回归模型
model = LinearRegression()
# 用数据样本训练模型
model.fit(X, y)
# 用训练好的模型去预测样本
predictions = model.predict(X)
# 打印输出
print('预测:', predictions)
print('系数:', model.coef_)
print('截距:', model.intercept_)输出结果:
预测:[1. 2. 3. 4.]
系数:[0.25 0.25]
截距:0.24999999999999956这段代码是对 X 数组中的数据进行线性回归模型拟合, y 数组作为目标变量(因变量),可以看出X有4个样本点,每个样本有2个特征,会自动学习出2个回归系数和1个截距,最终的训练模型为y=0.25+0.25x1+0.25x2。
这里特别说明的是,虽然上面的代码简单,但现在的机器学习库的使用流程基本都是一样的:先从库(sklearn)中导入需要的模型(LinearRegression),然后导入数据进行训练(fit),最后便可以使用训练好的模型对新数据进行预测(predict),如果觉得有需要,可以查看模型的关键参数(coef_和intercept_ )。下文所有算法模型的建模流程都是遵循这种三板斧流程,不再赘述。
不过一般情况下,训练模型用的数据集称为训练集,给训练好的模型进行预测的数据集称为测试集,两个数据集一般数据是不重叠、没有交集的,咱这里是偷懒了,请注意区分。
二、逻辑回归(Logistic regression)
不要看到这个算法里面有“回归”(regression)的字样,就以为它是像线性回归那样用来完成回归任务的,其实它主要是被用来完成分类任务的。通常是基于一个或多个自变量预测二元结果的概率。
它的模型结构是y=1/(1+exp(a0+a1*x1+a2*x2+...+an*xn)),就是在线性回归的基础上,套上了一层Sigmoid函数y=1/(1+exp(x)),无论exp(*)当中的数值是什么范围,都能将y限制到0~1之间,很好地完成二分类任务。
在金融投资和量化交易领域中,逻辑回归就是经常被用于分类任务,例如证券价格是上涨还是下跌、财务报表当中是否存在欺诈行为或者企业净利润率是否超额上升。
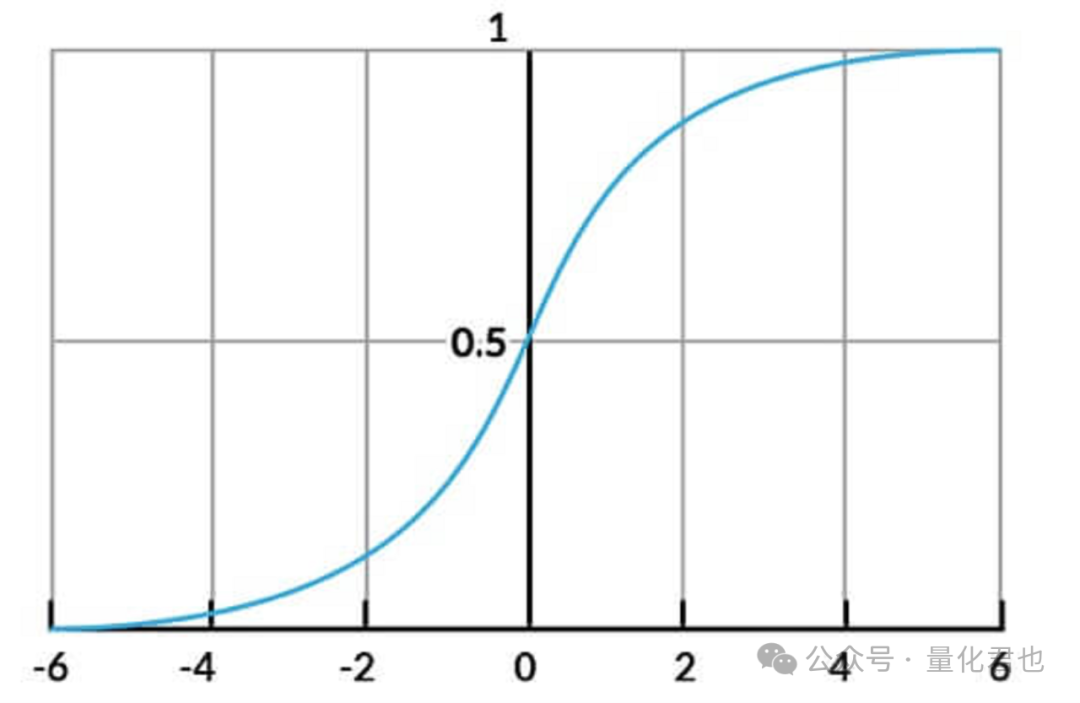
逻辑回归的主要优势和线性回归一样,实现和解释起来都相对简单,即使在大型数据集上训练也非常快速。除此之外,逻辑回归具有“概率性”的特性,这意味着它可以输出概率形式的预测结果,而不仅仅是二元预测,这一点在量化交易当中非常有用,能衡量其中不确定性或风险水平。
咱来看看逻辑回归的使用实例,如下所示,从整个流程来看,跟线性回归模型是一样的,只不过对于分类任务,y的标签数值要改为0或1,用来表示类别。
import numpy as np
from sklearn.linear_model import LogisticRegression
# 构建数据样本
X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
y = np.array([0, 1, 0, 1])
# 创建逻辑回归模型
model = LogisticRegression()
# 训练模型
model.fit(X, y)
# 对数据进行预测量
predictions = model.predict(X)
# 打印预测结果
print(predictions)三、决策树(Decision trees)
决策树之所以被称为“决策”树,顾名思义,能根据数据集的特征进行预测,它通过数据构建一个类似树状的决策模型来工作,每个分支代表不同的决策或结果。
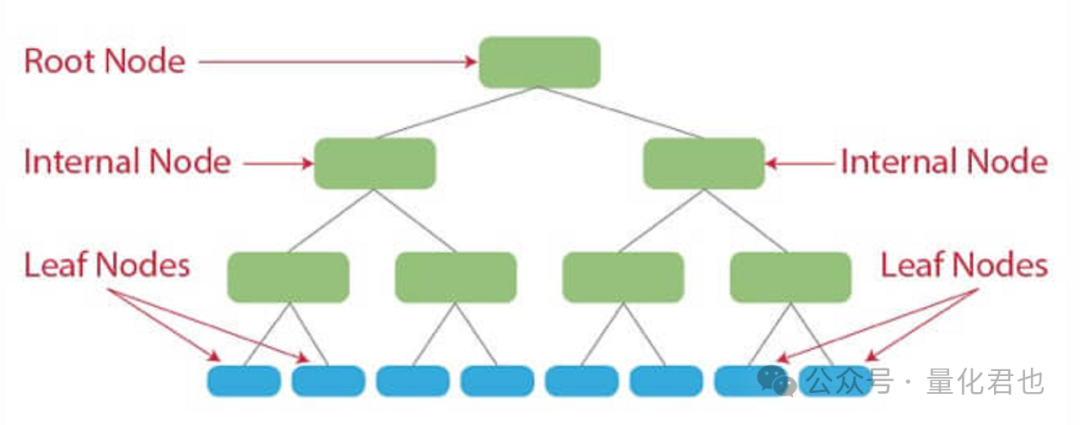
在金融投资和量化交易领域中,决策树通常被用于分类任务。决策树的主要优势除了相对简单易懂和解释较强外,关键它还能够处理复杂的数据集,并能够识别特征与目标变量之间的非线性关系。不过,如果决策树没有经过适当的修剪,可能会出现过拟合的问题,从而降低其泛化能力。
决策树的使用案例如下所示,流程跟上面两种算法是一样的,注意是分类任务就好。
import numpy as np
from sklearn.tree import DecisionTreeClassifier
# 构建样本数据
X = [[0, 0], [1, 1]]
Y = [0, 1]
# 创建决策树分类器
clf = DecisionTreeClassifier()
# 训练模型
clf = clf.fit(X, Y)
# 打印预测结果
print(clf.predict([[2., 2.]]))对了,你还可以指定用于拆分树的准则类型,例如“gini”或“entropy”,并设置其他参数,如树的最大深度或叶节点所需的最小样本数,在scikit-learn文档中可以找到完整描述。
https://scikit-learn.org/stable/modules/tree.html
四、随机森林(Random forests)
随机森林属于上面刚介绍的决策树的扩展,基于集成学习的原理,用于进行更强大和可靠的预测。它通过创建一组决策树,并使用每棵树所做预测的平均值来进行最终预测,就类似于现实当中咱一群人投票,然后少数服从多数那样。
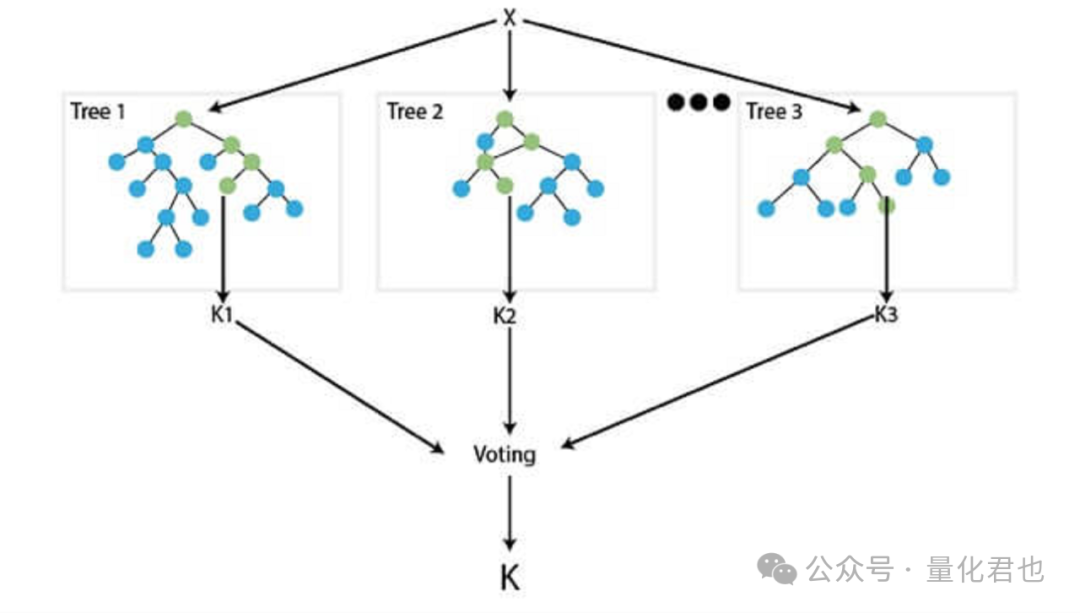
随机森林一般也是被用于分类任务,一般具有比较高的准确性,并且往往比单个决策树具有更好的泛化能力。不过,与单个决策树相比,随机森林的解释性相对差一些,因为预测是基于许多树的平均值,而不是单个树。
在使用当中,从sklearn里面导入 RandomForestClassifier 模型后,需要设置森林中树的数量(n_estimators ),树的最大深度(max_depth)和随机种子(random_state),其他的部分,就是跟传统的三板斧流程一样的了。
import numpy as np
from sklearn.ensemble import RandomForestClassifier
# 加载训练集和测试集数据
X_train, y_train, X_test, y_test = load_data()
# 创建随机森林模型
model = RandomForestClassifier(n_estimators=100, max_depth=2, random_state=0)
# 训练模型
model.fit(X_train, y_train)
# 预测新数据
predictions = model.predict(X_test)
# 打印预测结果
print(predictions)需要特别说明的是,load_data()是抽象出来的函数,需要自己根据自身应用情况实现,主要目的是用来加载训练集数据(X_train)和标签(y_train)、测试集数据(X_test)和标签(y_test),组织形式跟上面介绍过的3个算法是一样的,如果当前自己还没有确切建模任务的话,可以根据我之前的两篇文章《手把手教你,利用机器学习模型,构建量化择时策略》和《投资经理3周须开发4000个量化因子,手把手教你4行核心代码轻松应对》中的数据准备部分构建因子数据和打上对应的标签。
如果也不想自己组织数据,想马上就开箱使用,那可以直接使用sklearn机器学习库datasets模块,里面自带了各种机器学习任务需要用到的数据集,首先你可以使用make_regression或make_classification函数自定义生成自己需要的回归/分类数据集,其次你也可以使用现成的数据集,例如回归任务常用的糖尿病数据集(load_diabetes),分类任务的鸢尾花数据集(load_iris)。
就以随机森林这次的分类任务为例,使用鸢尾花数据集(load_iris),咱先看一下具体的数据形式。
import numpy as np
import pandas as pd
from sklearn import datasets
iris = datasets.load_iris() # 导入鸢尾花数据
data = iris['data'] # 数据
label = iris['target'] # 数据对应的标签
feature = iris['feature_names'] # 特征的名称
df = pd.DataFrame(np.column_stack((data,label)), columns=np.append(feature,'label'))
df.iloc[[0,1,60,61,120,121],:] # 分别展示类别为0、1、2的样本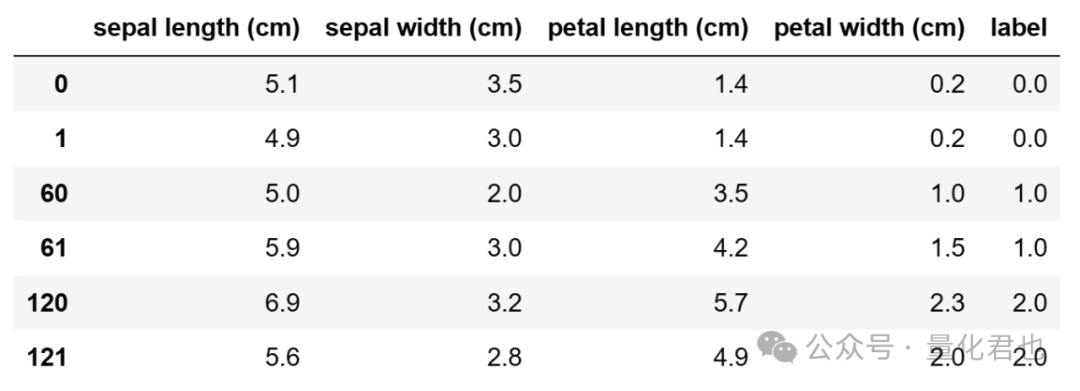
iris包含了 150 个鸢尾花的数据,其中每个样本有 4 个特征,分别为萼片长度、萼片宽度、花瓣长度和花瓣宽度,以及对应的类别标签,label的0、1、2分别对应花的品种Iris Setosa、Iris Versicolour、Iris Virginica)。
于是乎,要在随机森林当中使用这个数据集来训练和测试模型,只需要将应用实例当中的这句代码
# 加载训练集和测试集数据
X_train, y_train, X_test, y_test = load_data()修改为
from sklearn import datasets
from sklearn.model_selection import train_test_split
# 加载训练集和测试集数据
iris = datasets.load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2)为了方便阐述和展示,下文依旧使用抽象函数load_data()表示训练集和测试集数据的加载,不再赘述。
五、K最近邻(KNN)
K最近邻(K-Nearest Neighbors,KNN)是一种常用于分类和回归任务的机器学习算法,它大概的原理是通过找到离给定数据点最近的K个数据点,并利用这些数据点的类别或数值来进行预测。相信大多数人都听过这种说法,“你的收入就是身边 5 位好友收入的平均值”,KNN贯彻的就是这种“人以群分,物以类聚”的理念。
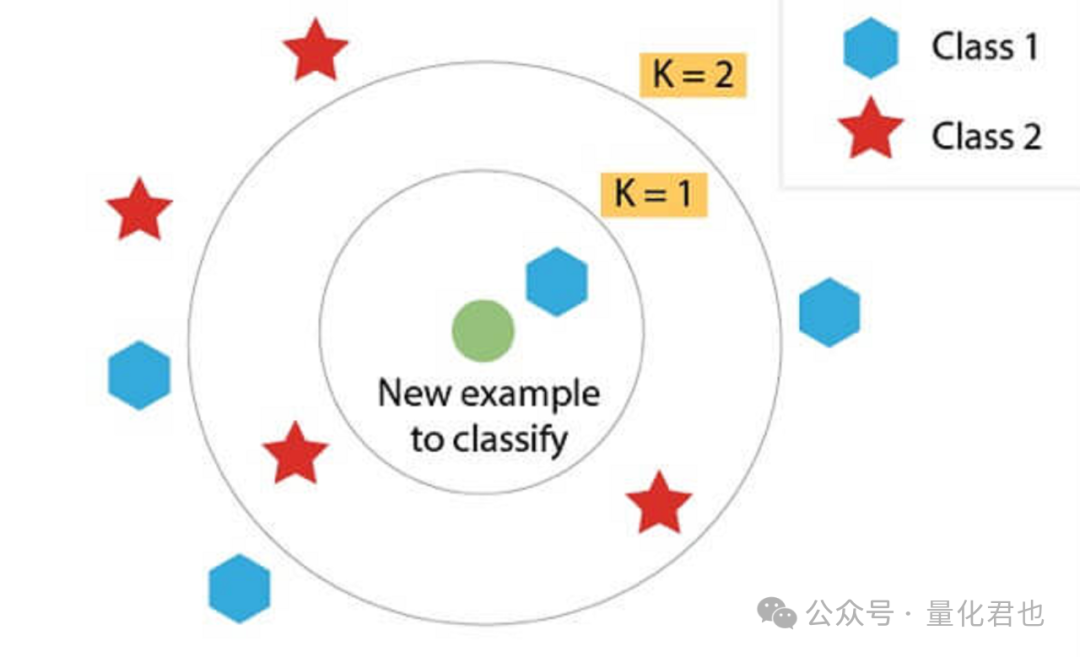
在金融投资和量化交易领域中,KNN通常用于分类任务居多,也可以用于回归。KNN的主要优势之一是相对简单易懂,并且容易实现,对缺失值不太敏感,最大的缺点就是,它对于K值的选择比较敏感。除此之外,在特征/因子数量相对于样本数量过大的情况下可能表现比较拉胯,在大型数据集上进行KNN预测也可能需要比较大的计算量。
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
# 加载训练集和测试集数据
X_train, y_train, X_test, y_test = load_data()
# 创建KNN模型
model = KNeighborsClassifier(n_neighbors=5)
# 训练模型
model.fit(X_train, y_train)
# 预测新数据
predictions = model.predict(X_test)
# 打印预测结果
print(predictions)六、K均值聚类算法(K-Means)
说完KNN,就顺道儿来说一下它的亲戚K-Means,从称呼上看起来很像,底层原理也很像,但干的却是不一样的活儿。
K-Means一般用于聚类(clustering)任务,而KNN一般用于分类(classification)任务,虽然是一字之差,但用途却不一样。咱可以先把实例代码贴出来,你就会发现它跟别的算法代码有个显著的区别。
import numpy as np
from sklearn.cluster import KMeans
# 构建样本数据
X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])
# 创建KMeans模型
model = KMeans(n_clusters=2, random_state=0, n_init='auto')
# 训练模型
model.fit(X)
# 预测新数据
predictions = model.predict([[0, 0], [4, 4]])
# 打印预测结果
print(predictions)看见木有,别的算法一般训练模型时都需要同时输入特征/因子数据X和标签数据y,而K-Means只需要输入特征/因子数据X,前者这种训练方式被称为监督学习(Supervised learning),后者则被称为无监督学习(Unsupervised learning),前者就相当于让你自学的时候,既发给你试题,也发给你参考答案,后者是只发试题,木有答案。
那有什么用呢?也是起到“人以群分,物以类聚”的划分作用,因此K-Means叫聚类算法,比如说现在A股有5000多支股票,申万把它们划分为31个行业,你觉得这样划分不合适,可以给它们设定不同的属性/因子和想分成多少个行业/概念/风格/板块(例如上面实例的聚类数是2),K-Means算法就可以把这5000多支股票按自己的要求划分出来,在每个簇当中,里面的股票在你设定属性/因子方面肯定都是极其相似的,属于你自己的行业/概念/风格/板块。很多时候,你会惊叹,八竿子打不着的股票怎么会在这些方面这么相似。

七、支持向量机(SVM)
支持向量机(Support Vector Machines,SVM)最初的设计是用来解决二分类问题,后来扩展到多分类问题,比如说之前开发的大盘择时策略“预测沪深300指数涨跌”就属于典型的二分类问题,“涨”是一个类别,“跌”就是另一个类别。
它通过寻找一个最大间隔超平面将两类样本线性区分开来,并且保证两侧样本的最近边缘点到这个平面的距离是最大的,由于最大间隔超平面仅取决于两个类别的边缘点,这些点就被称为支持向量,这就是“支持向量机”名称的由来。
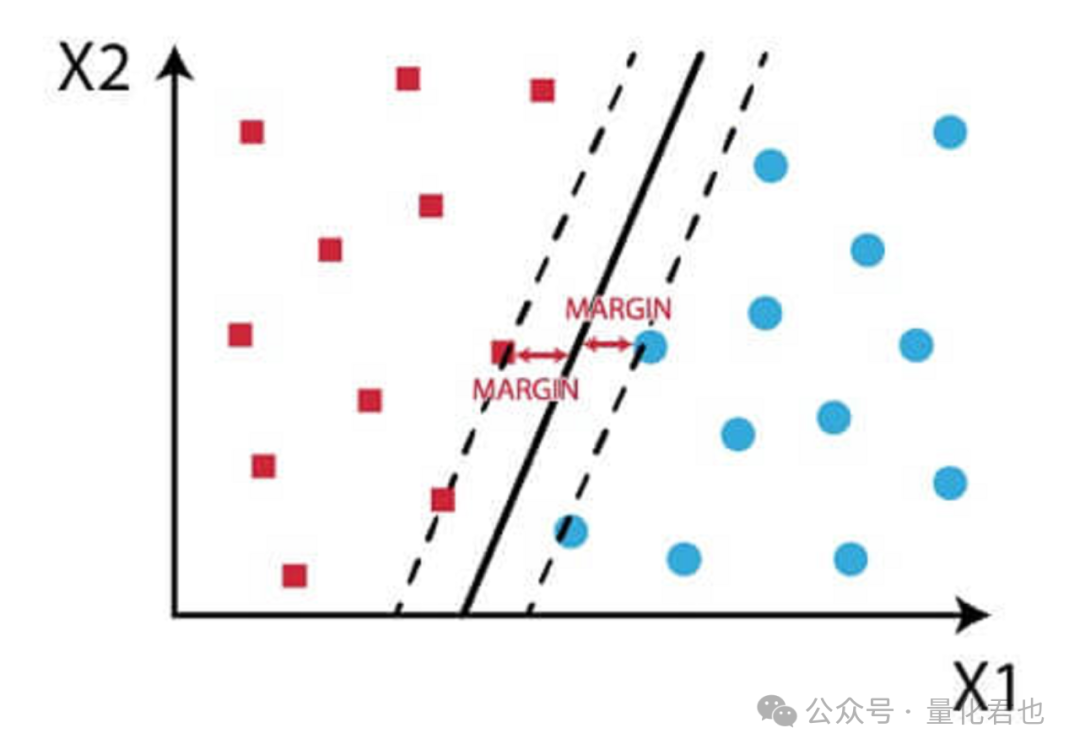
如果数据点在原始空间不可分的话,就将低维不可分的数据映射到高维线性可分,于是乎,SVM的主要优势之一就是能够处理高维数据,并且能识别特征与目标变量之间的复杂关系。
不过,与其他一些机器学习算法相比,SVM的训练计算量可能更大,并且由于基于复杂的优化问题,解释性就相对差一些。对了,为了将数据从低维映射到高维,SVM中核函数的选取就非常关键,常用的核函数有线性核、多项式核、高斯核(RBF核)和Sigmoid核。
import numpy as np
from sklearn.svm import SVC
# 加载训练集和测试集数据
X_train, y_train, X_test, y_test = load_data()
# 创建SVM模型
model = SVC(kernel='linear', C=1.0)
# 训练模型
model.fit(X_train, y_train)
# 预测新数据
predictions = model.predict(X_test)
# 打印预测结果
print(predictions)八、朴素贝叶斯(Naive Bayes)
朴素贝叶斯是一种基于贝叶斯定理进行预测的机器学习算法,它之所以被称为“朴素”是因为它假设数据集当中的所有特征都是相互独立的,而在现实世界的数据中当然肯定不是这样的。
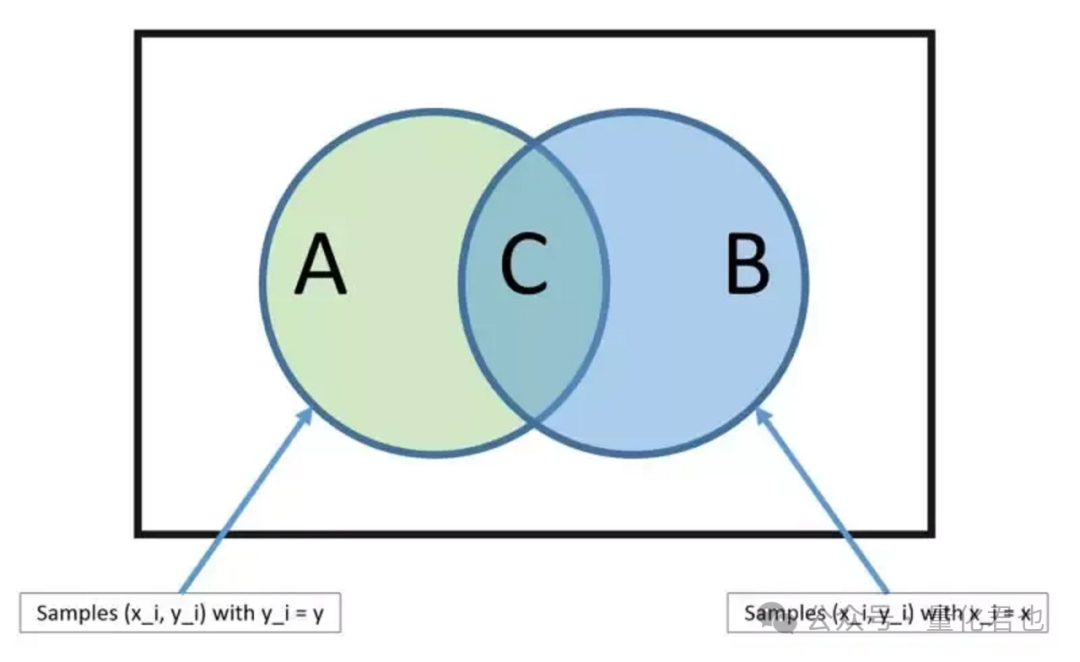
尽管有这个假设,朴素贝叶斯算法通常用起来效果也不错,并且在金融投资和量化交易当中经常使用。朴素贝叶斯算法常被用于分类任务,比如预测指数第二日涨跌、财经新闻的正负面情或者财务报表是否掺假。
朴素贝叶斯算法的主要优势之一就是其简单性和易于理解了,就连很多成功学文章和书籍中,都经常倡导要“贝叶斯式”思考。这个模型训练起来也非常快,即使是在大型数据集上。并且,当底层数据受到某些类型的噪声干扰影响,或者特征数量相对于样本数量过大时,朴素贝叶斯算法往往也都有良好表现。
import numpy as np
from sklearn.naive_bayes import GaussianNB
# 加载训练集和测试集数据
X_train, y_train, X_test, y_test = load_data()
# 创建朴素贝叶斯分类器
model = GaussianNB()
# 训练模型
model.fit(X_train, y_train)
# 预测新数据
predictions = model.predict(X_test)
# 打印预测结果
print(predictions)九、神经网络(Neural networks)
神经网络是一种受到人脑结构和功能启发而研发出来的机器学习算法,模型结构由大量相互连接的节点(神经元)组成,模拟人脑的机制用于处理和传输信息。神经网络特别适用于涉及模式识别和预测的任务,并且已被广泛应用于各种领域和场景,取得了非常显著的成果。
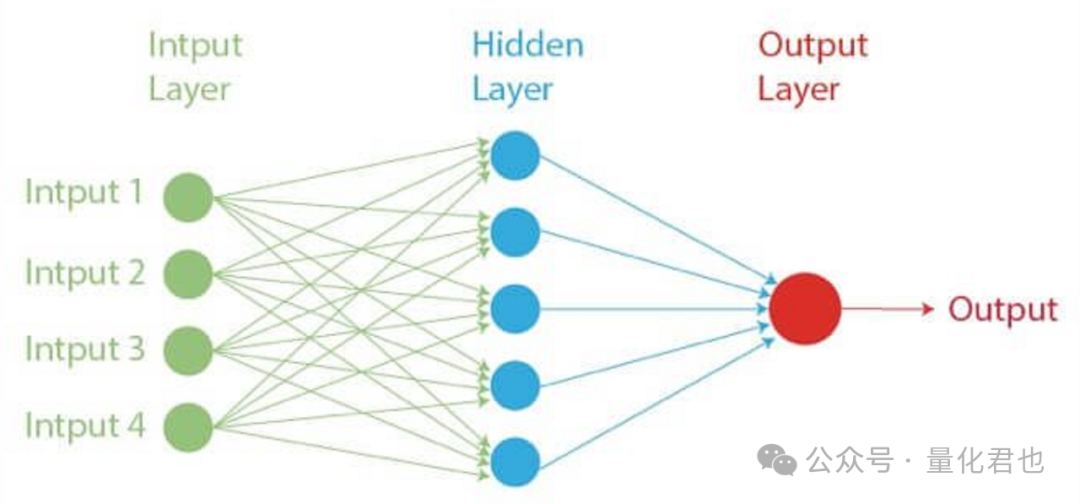
神经网络模型在回归和分类任务上都非常支棱,只需要人为地确定模型结构,然后就能够在没有显式编程的情况下学习、迭代和适应新数据,它还可以处理大型和复杂的数据集,并能够识别特征与目标变量之间的非线性关系。
与其他一些机器学习算法相比,神经网络的训练可能需要消耗更多的计算资源,并且由于其中复杂的网络结构,因此可解释性就差很多,如果设计和训练不当的话,神经网络非常容易过拟合。
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# 加载训练集和测试集数据
X_train, y_train, X_test, y_test = load_data()
# 创建神经网络分类器
model = Sequential()
model.add(Dense(8, input_dim=4, activation='sigmoid'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# 训练模型
model.fit(X_train, y_train, epochs=20, batch_size=32)
# 预测新数据
predictions = model.predict(X_test)
# 打印预测结果
print(predictions)十、集成学习(Ensemble learning)
集成学习(Ensemble learning)并不是特指某一个算法,而是一个算法大类,或者说是训练和组合模型的思路或方法。在机器学习当中,单个模型运行时可能表现没那么好,但同时将多个模型组合起来,“三个臭皮匠顶个诸葛亮”,就会变得非常强大,这种多个基础模型/算法的组合,就被称为集成学习。
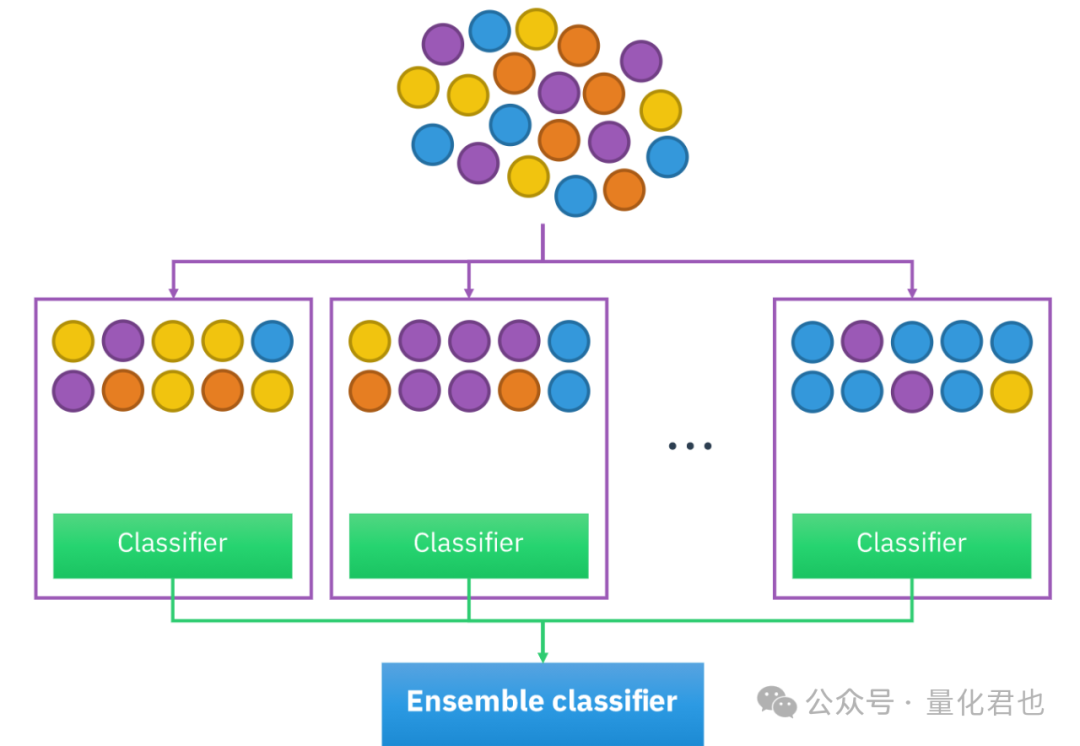
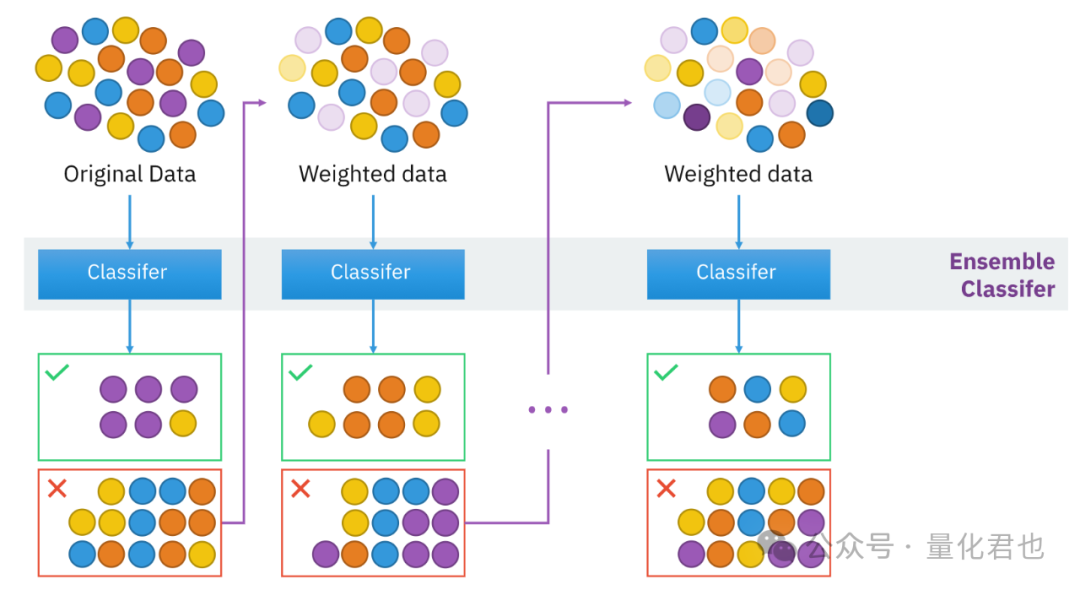
集成学习一般分为两大类:Bagging(装袋法)和Boosting(提升法)。这两种方法都是将多个弱模型组合在一起,形成一个强模型,但它们之间最明显的区别是,Bagging中的多个弱模型都是并行单独训练,然后再组合在一起,而Boosting是串行训练,下一级弱模型是根据前一级弱模型的“残差”针对性训练,用来提升上一级的“短板”,最终再组合在一起。其实集成学习还有更为复杂的Stacking(堆叠法)和Cascading(级联法),有兴趣的话,可以自己去探究一下。
Bagging模型结构:
Boosting模型结构:
Bagging集成学习其实咱之前已经见过了,那就是随机森林,在金融投资和量化交易领域,Bagging用得最多的就是它。
Boosting集成学习就比较多了,常见的有:梯度提升树GBDT、自适应提升算法Adaboost、极限梯度提升算法XGBoost和轻量级梯度提升算法LightGBM。以前常用XGBoost组合多因子模型,现在多流行用LightGBM,那就以LightGBM作为实例展示吧。
import numpy as np
import lightgbm as lgb
# 加载训练集和测试集数据
X_train, y_train, X_test, y_test = load_data()
# 训练模型
gbm = lgb.train(params={'learning_rate': 0.05,
'lambda_l1': 0.1,
'lambda_l2': 0.2,
'max_depth': 3,
'objective': 'multiclass',
'num_class': 3},
train_set=lgb.Dataset(X_train, label=y_train))
# 预测新数据
predictions = gbm.predict(X_test)
predictions = [list(v).index(max(v)) for v in predictions]
# 打印预测结果
print(predictions)量化交易领域的10大常用机器学习算法就盘点完了,不知道你有没有发现,再复杂的机器学习算法,利用现成的机器学习算法库(如sklearn),按照“三板斧”流程,十几二十行代码就可以建模完毕,麻麻再也不用担心咱的算法实现。
这就是本文想要达到的目的,以后大伙儿大部分时间只需要专注于量化任务拆解和数据整理,是分类任务(如预测涨跌),还是回归任务(如预测涨跌幅),接着把特征/因子数据整理好,按照这篇“机器学习算法清单”的索引,按需按代码实例使用相应算法就搞掂了,顺藤摸瓜,按图索骥。
内容来源/参考:
Christophe Atten,2022.12,《Top 10 machine learning algorithms in Finance》
Chainika Thakar,2023.01,《Top 10 Machine Learning Algorithms For Beginners》
机器之心,2019.03,《机器学习必学10大算法》
楷哥,2020.10,《集成学习》
周志华,2016.01,《机器学习》
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
