作者:麦教授随笔
题图:麦教授随笔微信公众号

最近总有人问我们一个问题:你们在春节前别的量化机构都大幅回撤的时候为什么能做到还是正超额?
我其实在过去几年的路演中多次讲到了底层逻辑,能看懂我公式的自然就懂了,但是看不懂公式的,有没有办法解释清楚呢?
这篇文章就是在不写公式的前提下讲清楚我们是怎么理解风控的。
“正确的思考方式是Zeckhauser打桥牌的方式。就是这么简单。聪明人会做出可怕的蠢事……也许像Zeckhauser这样伟大的桥牌手不会,但这是经过训练的反应。”——查理·芒格
芒格称赞的这个人是美国经济学家、哈佛大学肯尼迪学院政治经济学教授Richard Zeckhauser,他是桥牌冠军,也被誉为“概率先生”。
为什么芒格会用「伟大」来形容他?在Zeckhauser的论文《Investing in the Unknown and Unknowable》中,我们可以找到一些关于「正确思考方式」的线索。论文的标题在当下的环境也显得尤为贴切。
这里主要介绍论文中对风险(risk)、不确定性(uncertainty)和无知(ignorance)的讨论。
任何投资都存在一定程度的「风险」和「不确定性」,二者常被混为一谈,但它们之间有明显的区别。
来看这两个例子。
1)掷两个骰子一百万次,根据大数定律,骰子落在2的概率为2.78%,落在 7 的概率为 16.67%,这是一个确定的系统。

2)预估10年期利率的未来走向或是未来10年甚至1年后的宏观大局。这是一个不确定的系统。
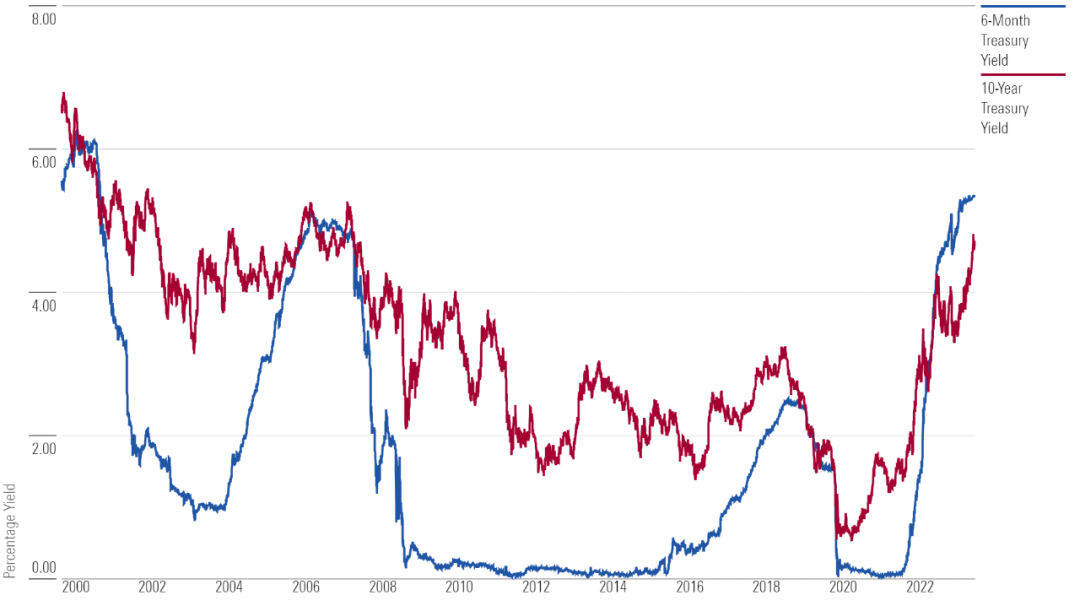
风险是一种概率被明确定义的情况,它的重要性远不如不确定性。依赖骰子、纸牌和机械设备的赌场,以及拥有大量数据储备的保险公司,有充分的理由考虑风险。但我们大多数人只有在愚蠢到去赌场或购买彩票时才需要担心风险……——Richard Zeckhauser

可见,「风险」表示概率已知或可知。然而,生活中却鲜有纯粹是「风险」的情况,大多数结果都介于「风险」和「不确定性」之间的某个范围内。
Zeckhauser认为,应对「不确定性」比应对「风险」重要得多。因为「风险」可以管理,「不确定性」无法管理,但它可以被转化为「风险」。(这一点稍后会再讨论。)
“我们经常面临的困难是「不确定性」,而不是「风险」。即我们可以识别世界的状态,但不能识别它的概率。[……]我们现在应该明白,许多通常被定义为涉及「风险」的现象——尤其是2008年之前金融领域的现象——实际上涉及「不确定性」。”——Richard Zeckhauser
根据状态能否被识别与概率是否可知,「风险」就是“已知的已知”(known knowns),「不确定性」则是“已知的未知”(known unknowns)。
而对于状态和概率都未知且不可知的情况,Zeckhauser用“无知”(ignorance)来表示,即“未知的未知”(unknown unknowns)或“未知与不可知”(unknown & unknowable)。
“当世界上某些潜在状态无法被识别时,就会产生「无知」。我认为,「无知」是一种重要现象,与「不确定性」并列于「风险」之上。「无知」之所以如此重要,不仅是因为它普遍存在,而且还因为它带来了重大后果。人们无法明智地为世界的未知状态分配概率。正如传统金融理论在遇到「不确定性」时会碰壁一样,现代决策理论在处理「无知」世界时也会碰壁。”——Richard Zeckhauser
地缘政治、金融危机或气候灾难等事件的未来走向或状态都属于「无知」的范畴。因此,与「风险」和「不确定性」不同,「无知」无法用模型评估。

△Zeckhauser用来解释「风险」「不确定性」和「无知」的图表
来自「不确定性」与「无知」领域的事件往往影响重大,并且会给投资者带来巨大的困难与挑战,但Zeckhauser也指出了积极的一面。
“第一个积极的结论是,不可知(unknowable)的情况已经并将继续带来巨大的投资回报。第二个积极的结论是,有系统的方法来思考「不可知」的情况。如果遵循这些方法,就能获得非凡的预期投资回报。诚然,有些重大损失是不可避免的,有些损失在事后应受谴责。但即使考虑到风险规避因素,净预期结果也将是非常积极的。”——Richard Zeckhauser
换句话说,即使未知的未来不可预测,仍然可以为之做好准备。这些准备涉及对概率的认知。
Zeckhauser表示,如果金融世界主要是一个充满「不确定性」的世界,那么最大的成功将属于那些最有能力评估概率的人。
“建立在正态分布假设基础上的投资组合理论是一栋美丽的大厦,但在现实的金融世界里,尾部比正态分布的预测要肥厚得多。当未来的价格取决于数百万人的选择,以及这些人对当前价格和近期价格变动的反应时,我们就不再处于不受非理性感染的保护伞之下了。典型的羊群行为(偶尔出现踩踏事件)在解释重要的价格走势方面优于布朗运动。”——Richard Zeckhauser
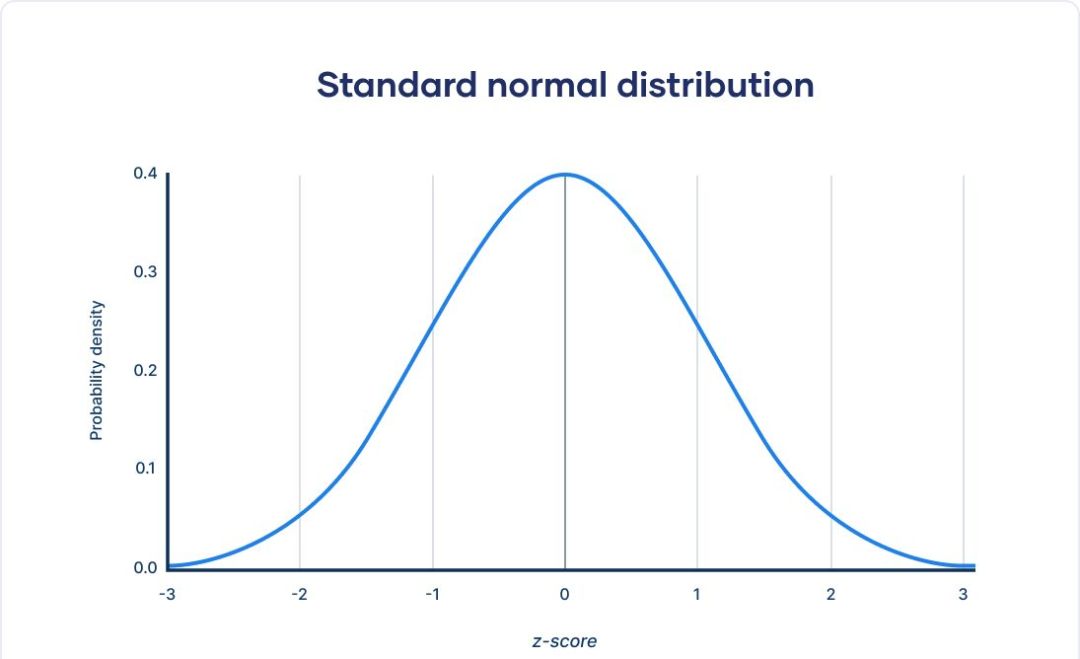
△正态分布
在研究金融市场中的概率问题时,一种错误的思维模式是:自动从正态分布或布朗运动的角度思考问题。在此基础上,依赖历史,或是建立在错误假设之上的模型都不可靠。
在快速创新的推动下,根据模型的推论,那些应该每百年或千年才发生一次的事件却在越来越短的时间跨度内发生,每次危机的起因都各不相同,下一场危机也将与过去的危机大不相同。

△布朗运动
须知市场是复杂适应系统(Complex Adaptive System),这种复杂性并不适合简洁的数学。也就是说,黑天鹅会比预期中的更多。
这意味着两点。
首先,重大的投资错误往往发生在极端情况下,无论市场是陷入恐慌还是处于兴奋的高点。为极端情况做好准备,才能在「无知」中游刃有余。
其次,要接受「不确定性」的存在。有时危机是无法避免的,所以不该低估危机来临时对人类理性的冲击。忽视「不确定性」会招致更多的「无知」。
当然,Zeckhauser也给出了应对「风险」、「不确定性」和「无知」的思路。
对于「无知」
应对「无知」的关键在于察觉它的存在。
一旦意识到处于「无知」状态(比如试图预测另一场大流行病或战争,或是下一次金融危机何时到来时),就应该改变对世界和当前形势的思维模式,并在必要时采取理性行动来做好准备。
“我们无法通过告知银行需要额外保留十亿美元左右的准备金来预防最有可能发生的下一次金融危机。但我们应该时刻警惕新的风险。[…]我们可能会遇到这样的情况:损失的预期从100下降到50,发生危机的可能性从1%下降到0.5%。但危机还是会发生,一旦发生,损失就是50。如果能够将车祸的可能性和严重程度降低一半,就可以将车祸死亡人数减少75%。这并不完美,但非常可喜。预防金融危机是不可能的,但降低其发生的可能性和严重程度将使全世界受益匪浅。”——Richard Zeckhauser
对于「不确定性」
相比于「无知」,「不确定性」更容易应对。因为它不仅可以被识别,还可以被降低甚至消除。
第一步是明确问题是否真的属于「不确定性」领域。这一点可以通过查看所在系统的复杂性做到。
「确定性」事件与「不确定性」事件的区别在于能否确定其概率分布。
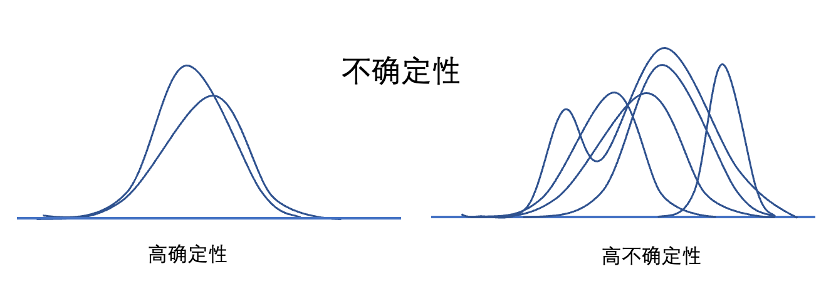
系统的「不确定性」则取决于两个因素:它的复杂性和你的理解程度。
系统越复杂,遇到「无知」的可能性就越大。
掷骰子实验是一个简单、孤立的系统,而预测利率则是一个复杂的系统,因为它受到数百万个外部动态变量的影响。在后一种情况下,就其「不确定性」而言,对系统的理解并不重要。但是,当处理的事情介于这两种极端情况之间时,就可以通过增加对系统的了解来减轻或消除「不确定性」。
越是远离复杂性,对系统的理解就越重要,对事物的理解越深,它的「不确定性」就越小,直到能够有效评估其「风险」。
“有效投资的本质是了解世界状况明确时表现良好的资产。[...]通过实践和对问题的认识都可以提高决策绩效。”——Richard Zeckhauser
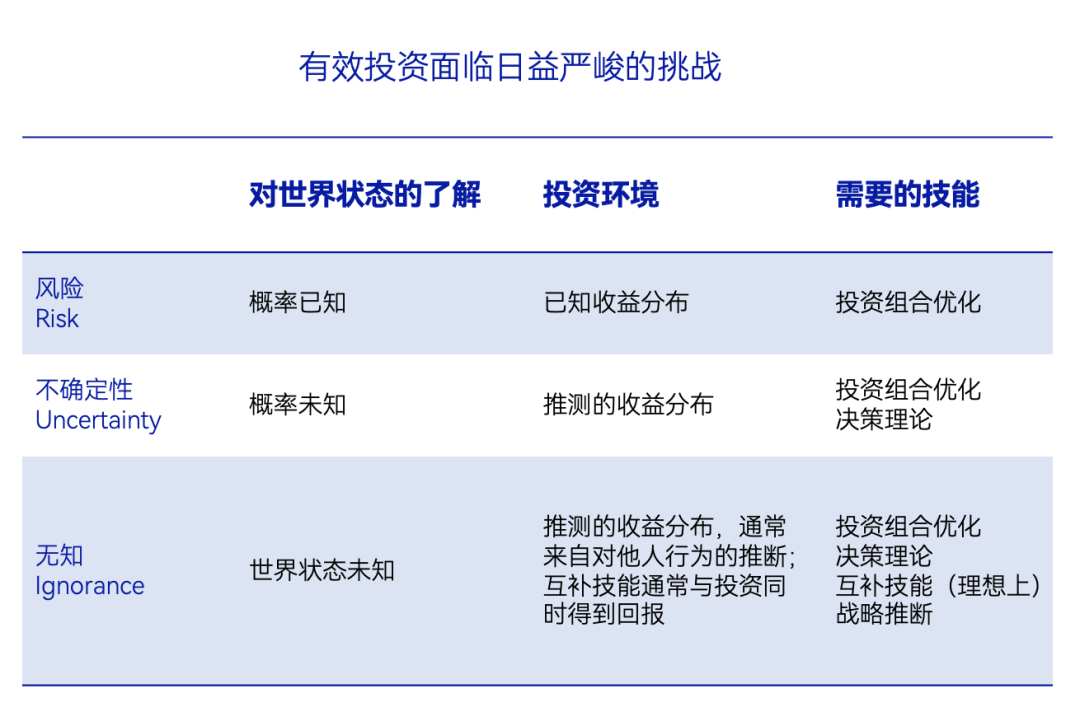
△Zeckhauser对有效投资的分析
某种程度上,「不确定性」是投资者的朋友。如果每个人都已知一切,就不会存在任何错误定价的套利空间。所以相应地,如果能减少「不确定性」,比其他市场参与者更多地了解未来结果的潜在范围,就能在市场中占据优势。
“投资者最好把时间花在获取「可知」的知识优势上:行业、公司和证券。你的关注点越微观,你就越有可能学到别人学不到的东西。”——Howard Marks
对于「风险」
由于「风险」是指能在一定程度上确定未来结果的概率分布,所以它最容易处理。

只要知道概率分布,风险就完全可控。比如轮盘赌,当你知道自己永远不会比庄家占优势时,就不会玩这个游戏。
投资也是同样的道理,只不过投资固有的「不确定性」因素可能会影响判断。如果可以消除其中所有的「不确定性」,只留下「风险」,投资决策也会变得简单。
需要注意的是,每项投资都包含一定程度的「风险」,这是无法消除的。重点在于能否定义「风险」以及明确「风险」在哪里偏斜。
Zeckhauser(还有大家熟悉的塔勒布)把这些问题都提炼的非常好,但是这个问题提出来之后怎么解决呢?
在我看来,提出问题是解决问题的第一步,即便你无法写出复杂的数学模型来做推导,能静下心来理解这些概念的不同,也会有非常大的收获。
理解投资中的「风险」、「不确定性」和「无知」后,你会发现:
在终极的分析中,一切知识都是历史.
在抽象的意义下,一切科学都是数学.
在理性的世界里,一切判断都是统计.
……
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
