Cross-Section Research, Looking Forward

作者：川总写量化

题图：川总写量化微信公众号

摘要

机器学习和大数据时代，资产预期收益截面差异研究的统一框架。

早先的文章《Cross-Section Research, A History》回顾了自上世纪 60 年代以来关于股票预期收益率 cross-section 的研究，包括 CAPM 以及后来的 FF3、q-factor model 这些 ad-hoc 多因子模型。该文的最后同时引出了当下流行的动态 latent beta factor model 框架：

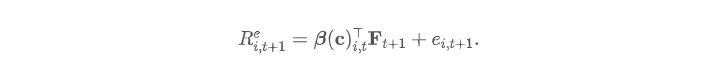
在这个框架中，因子是 latent，建模的对象是资产对因子的暴露 β ，而 β 是 firm characteristics c的线性或非线性函数，函数的具体形式和参数可以通过机器学习算法，以最小化资产的定价误差为目标函数来估计。

鉴于 beta pricing model 和 stochastic discount factor（SDF）的等价性，本文从 SDF 的角度进一步梳理这个统一的研究框架，它能够将当下众多基于机器学习的实证资产定价模型纳入其中，代表了 cross-section research 的未来。

1

在解读框架之前，首先要回答的是为什么需要框架。这个问题的答案是：新时代的实证资产定价研究是以大数据为依托、以机器学习算法为工具，围绕资产定价理论展开；而非将数据无脑扔进高级算法，单纯指望数据发声。因此，唯有放在框架下探讨前沿进展，才能理解不同方法之间的共性和差异，从而将学术研究的最新发现映射到投资实务之中。

让我们从条件 SDF 说起：

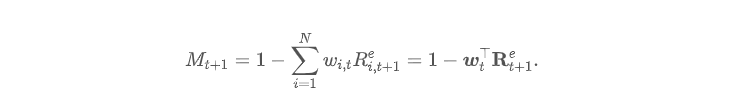
将权重 W_i，t 视为公司特征 C_i，t 的函数：

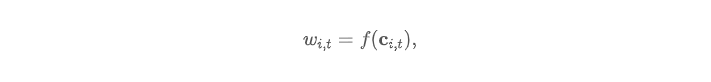
式中 f 是非线性函数， L 维向量 C_i，t 则表示 t 期公司 i 的公司特征取值。当然，f 是未知的。因此，为了构造 SDF，使用一系列 managed portfolios 来近似 f ：

式中， f_k（C_i，t）表示第 k 个 managed portfolio 中股票 i 的权重。值得注意的是，managed portfolios 的维数是 K ，它可以比 L 小很多。这些 managed portfolios 就是我们常说的因子。所以从因子的角度来说，SDF 可以是稀疏的，但是从原始变量的角度来说，SDF 并不稀疏。且这些 managed portfolios 可能是公司特征的非线性函数。

利用 managed portfolios，将原始 SDF 转化成如下静态模型：

上述模型之所以是静态的，是因为系数 b_k 不包含下标 t ，而模型的 dynamics 是通过 managed portfolios 中公司特征的变化来体现的。该静态模型就构成了我们的研究框架。不同的定价模型代表了真实 SDF 所包含的风险因子的不同先验。以人们熟悉的 Fama-French 三因子为例。在这个框架下，公司特征为 market cap 和 book-to-market ratio，而 f_k 为 double portfolio sort。

在这个框架下，新时代实证资产定价的研究目标为：以最大化 MVE 组合样本外夏普比率为目标，选择含有收益率预测信息的公司特征 c 、构造 managed portfoliosf_k 、以及估计 SDF 系数 b_k 。

以下两节分别探讨 c 和 f_k 两部分。而对于系数 b_k ，可通过 mean-variance optimization 叠加正则化的方式，确保样本外稳健的表现。

2

关于 c ，与股票预期收益率相关的协变量是高维的（量价数据、财务数据、分析师一致预期、舆情数据、另类数据），且协变量与预期收益率之间存在非线性关系，特别是协变量间的交互作用（例如，学界和业界常见的市值和另一个变量双重排序）。为了寻找协变量，学界的思潮主要围绕以下几个方面。

第一，针对多重假设检验问题进行调整（Harvey 2017，Harvey, Liu and Zhu 2016）。在这方面，尽管这几年更多的声音是学术发现大部分 are likely true（Jensen, Kelly, and Pedersen 2023），但我个人更支持 Harvey and Liu 的观点。对这个问题，根据经验和对数据的理解、使用合理的先验（即真实因子的百分比）才能得到对于投资实践有益的结论。而基于 ensemble null 假设的数学推导游戏（Chen 2021）毫无意义。

第二，投资者面临的高维学习问题（Martin and Nagel 2022）。理性预期假设投资者知道真实的估值模型。然而，投资者面临高维学习问题，不可能知道真实的估值模型。这会造成均衡状态下资产价格和理性预期情况下相比出现偏差。因此，在事后（ex post）分析中，已实现收益率中包含一部分因估计误差导致的可预测成分。而对投资者来说，事前（ex ante）无法利用上述可预测性。事后分析中发现的可预测性是虚假的。在这方面，最直观的例子就是将当下的技术手段所进行的高级数据分析应用于历史数据中，而历史数据那个时期并不存在同样的分析手段或者投资者使用该手段的成本极高。

第三，由 APT 可知，解释资产预期收益率的协变量应能解释资产的共同运动（Kozak, Nagel, and Santosh 2018）。所以，协变量应该和资产收益率的一阶矩以及二阶矩都有关。在这个背景下，同时考虑一阶矩和二阶矩信息的方法（例如 risk-premium PCA）取得了很好的实证结果。

3

再来看 f_k 。

传统的构造方法以来 portfolio sort（这主要归功于 Fama and French 的开创性工作）。而显然，在协变量的高维数时代，进行高维的 portfolio sort 是不切实际的。所以，当下的解决方案是 embrace machine learning。

然而，由于金融数据的信噪比极低以及不满足平稳性（即 alpha 会因为被交易掉而消失），导致 parameter scaling, regularization, cost function……每个选择都可能影响机器学习模型在样本外风险收益特征（Nagel 2021）。对此，学术界的一致观点是 off-the-shelf 的机器学习算法难以成功，而是要通过适当的途径注入经济学理论（例如使用贝叶斯框架）。例如，实证分析表明 ridge regression 比 OLS 在样本外能够获得更高的 R² 和 Sharpe Ratio。这是因为 Ridge regression 背后有优雅的贝叶斯收缩解释。

此外，No-Free-Lunch 定理对于资产定价研究同样适用。不同的模型和不同的协变量选择，代表了研究者关于 SDF 的不同先验，也会有不同的实证结果。仅仅以实证结果为依据来挑选模型只能陷入 model-hacking。

4

在本文所描述的框架下，我们很容易理解并比较近年来实证资产定价研究的最新发现。例如 Bryzgalova, Pelger and Zhu (2020) 的 asset pricing tree。该文通过 decision tree 构造 managed portfolios，而在估计权重系数 b_k 时，同时收缩 managed portfolios 的预期收益和协方差矩阵。又比如 Chen, Pelger and Zhu (2020) 使用生成对抗网络来构造 managed portfolios。此外，IPCA 或者 autoencoder 等模型则可以放在和 SDF 等价的 latent beta factor model 下来对比。在统一的框架下审视这些方法无疑会加深我们的理解。

让我们重申一下机器学习时代的实证资产定价研究。和传统的 ad-hoc 多因子模型以最小化样本内的 pricing errors 不同，它们以最大化样本外条件夏普比率为目标。机器学习算法可以同时处理大量解释变量、考虑变量和预期收益率的非线性关系，但使用时需施加经济学推理。近年来，学术界利用 SDF 框架或隐性因子模型范式，提出包含大量公司特征的定价模型，这种趋势代表了实证研究的未来。

最后，once again，一图胜千言。

参考文献

Bryzgalova, S., M. Pelger, and J. Zhu (2020). Forest through the trees: Building cross-sections of stock returns. Working paper.

Chen, A. Y. (2021). The limits of p-hacking: Some thought experiments. Journal of Finance 76(5), 2447–2480.

Chen, L., M. Pelger, and J. Zhu (2020). Deep learning in asset pricing. Management Science forthcoming.

Harvey, C. R. (2017). Presidential Address: The scientific outlook in financial economics. Journal of Finance 72(4), 1399–1440.

Harvey, C. R., Y. Liu, and H. Zhu (2016). … and the cross-section of expected returns. Review of Financial Studies 29(1), 5–68.

Jensen, T. I., B. T. Kelly, and L. H. Pedersen (2023). Is there a replication crisis in finance? Journal of Finance 78(5), 2465–2518.

Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models. Journal of Finance 73(3), 1183–1223.

Martin, I. and S. Nagel (2022). Market efficiency in the age of big data. Journal of Financial Economics 145(1), 154–177.

Nagel, S. (2021). Machine Learning in Asset Pricing. Princeton University Press.

版权声明：文章版权归原作者所有，部分文章由作者授权本平台发布，若有其他不妥之处的可与小编联系。