作者:嘟嘟的投研CheatSheet,好投学堂专栏作家
题图:嘟嘟的投研CheatSheet微信公众号
理解夏普,是基金评价人员掌握业绩指标分析的第一道坎。相较于单纯追逐收益,更应该关注“风险调整后收益”,这是我们走向成熟的开始。
关于风险调整后收益
衡量风险的角度多种多样,除了关注对称性风险的夏普以外,还有关注非对称性风险的Sortino,以及只关注最大回撤的Calmar。
三者的分子都是策略的年化收益率(假设无风险利率为0),区别主要在分母端。其中,Sortino只关注负回报的波动率(标准差),夏普同时关注正回报和负回报的波动率,Calmar则仅关注最大回撤。

三者当中Calmar是最不可靠的。因为最大回撤在数据集中只有一个数据点,其取值往往与数据集长度有关:产品存续时间越长,碰到的最大回撤便会越大,因此在实践中几乎没有参考价值,所谓高Calmar的产品终会随着时间流逝而消失。
至于Sortino的出发点虽然是好的,但现实中同样存在判断的难度:
如果某个产品Sortino很高,究竟是因为它有较高的夏普,还是它只是有较稳定的负回报,实际上夏普并不高?
因此,我的选择是:在使用夏普衡量风险调整后收益之后,再单独使用衡量收益对称性的偏度指标。
关于收益对称性的偏度
偏度(Skewness)是统计学中用于衡量概率分布的不对称性或“偏斜”程度的指标。
正偏(右偏):右侧尾部较长。多数数据集中在平均值左侧,少数极大值拉高了平均值。投资者可能面临大幅上涨的机会,但也有可能长期处于较低收益状态,这种分布在风险资产(如成长股)中比较常见。
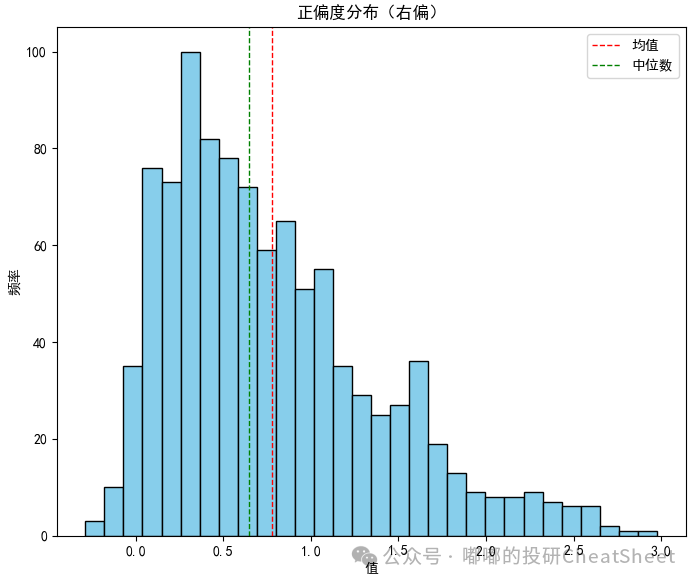
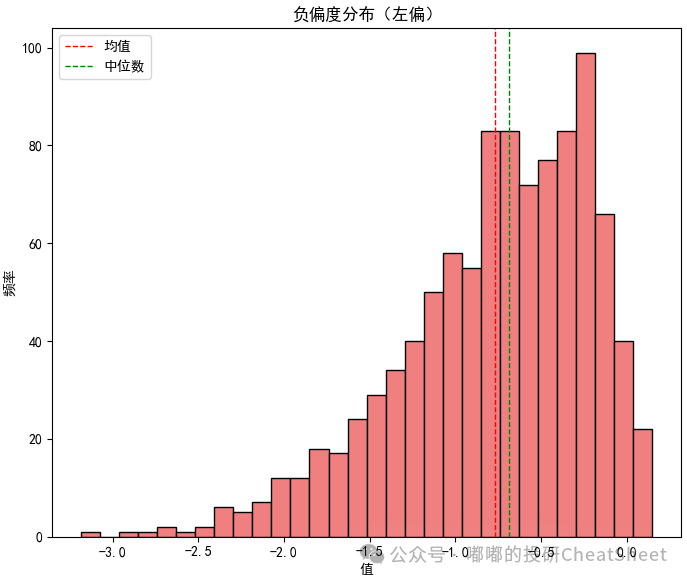
负偏(左偏):左侧尾部较长。多数数据集中在平均值右侧,少数极小值拉低了平均值。可以为投资者提供稳定的收益,但投资者可能面临突然大幅下跌的风险,这种分布在避险资产(如债券)中比较常见。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import skewnorm
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置字体为黑体
plt.rcParams['axes.unicode_minus'] = False # 解决坐标轴负号显示问题
# 生成正偏度分布数据
np.random.seed(0)
data_positive_skew = skewnorm.rvs(a=10, loc=0, scale=1, size=1000)
# 生成负偏度分布数据
data_negative_skew = skewnorm.rvs(a=-10, loc=0, scale=1, size=1000)
# 创建图形
fig, axes = plt.subplots(1, 2, figsize=(14, 6))
# 绘制正偏度分布图
axes[0].hist(data_positive_skew, bins=30, color='skyblue', edgecolor='black')
axes[0].set_title('正偏度分布(右偏)')
axes[0].set_xlabel('值')
axes[0].set_ylabel('频率')
axes[0].axvline(np.mean(data_positive_skew), color='red', linestyle='dashed', linewidth=1, label='均值')
axes[0].axvline(np.median(data_positive_skew), color='green', linestyle='dashed', linewidth=1, label='中位数')
axes[0].legend()
# 绘制负偏度分布图
axes[1].hist(data_negative_skew, bins=30, color='lightcoral', edgecolor='black')
axes[1].set_title('负偏度分布(左偏)')
axes[1].set_xlabel('值')
axes[1].set_ylabel('频率')
axes[1].axvline(np.mean(data_negative_skew), color='red', linestyle='dashed', linewidth=1, label='均值')
axes[1].axvline(np.median(data_negative_skew), color='green', linestyle='dashed', linewidth=1, label='中位数')
# 显示图形
plt.tight_layout()
plt.show()在此列举一些常见策略代表产品的偏度供参考,受样本选择影响可能会有较大区别:
- 趋势CTA:2.69
- 截面CTA:0.67
- 主观-成长:0.25
- 主观-价值:-0.55
- 主观-质量:0.19
- 量化转债:-0.01
- 量化指增:-0.41
- 量化中性:-1.93
- 期权波动率曲面:1.70
- 期权双卖:-3.10
- 债券:-2.00
站在我做资产配置的角度,是想追求0偏度的。一方面,我是典型的风险规避型投资者,0偏度意味着回报的波动性更小、极端值更少,收益和风险更加对称、均衡;另一方面,具有0偏度分布的产品,在使用VaR、波动率等风险管理工具时会更有效,因为上述工具通常假设收益分布是对称的。
目前我管理的两个组合:低波动的偏度为0.43,高波动的偏度为0.22
另外强烈推荐延伸阅读:《基研CheatSheet · 正负Gamma策略的平衡之道》。
关于风险的波动率
经常有人问我:嘟总你的策略最大回撤预期是多少?如前所述,这是一个无法回答的问题。我能告诉大家的是,产品的预期年化收益率和预期年化波动率,这里便产生了一个问题:如何将年化波动率与最大回撤关联起来?
以我的高波动复合组合为例,该组合长期目标年化收益率为15%、年化波动率(标准差)也是15%,在收益率满足正态分布的假设下(这便是为什么前面要讨论偏度),根据统计规律将满足68%-95%-99.7%规则,即:
- 约68%的收益位于年化收益±1个标准差范围内,即年化收益落在0%(15%-15%)至30%(15%+15%)的区间;在大约16%的时间里,我们的年化收益会在0%以下;在另外约16%的时间里,我们的年化收益会超过30%。
- 约95%的收益位于年化收益±2个标准差范围内,即年化收益落在-15%(15%-30%)至45%(15%+30%)的区间;在大约2.5%的时间里,我们的年化收益会在-15%以下。
- 约99.7%的收益位于年化收益±3个标准差范围内,即年化收益落在-30%(15%-45%)至60%(15%+45%)的区间;在大约0.15%的时间里,我们的年化收益会在-30%以下。
因此,对于上述夏普为1、年化波动率15%的产品,最大回撤达到15%甚至是30%,也完全是有可能出现的事情。
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
