作者:量化君也
题图:量化君也微信公众号
之前给大伙儿推荐过许多国外经典优质的量化干货,比如说《一大波国外高清量化网址正在袭来...》,都是有文章有源码、有图有真相的,但是有不少萌新小伙伴反映说看不懂、跑不通、用不上。
那咋办呢?东西是好东西,但没办法吸收,岂不是白瞎了嘛~
帮人帮到底,送佛送到西,扶上了马,还要送一程嘛。所以啊,我打算慢慢地把这些文章国产化本土化,这主要包含3个方面:
(1)将英文变成中文,并且用人话说出来;
(2)修改原始代码,让它在国内也能跑通;
(3)将测试标的换成国内的品种,熟悉还用得上。
大的修改主要是这3方面,更细节的就是我会在保证原版功能的情况下,根据个人经验调整代码的实现方式以及部分参数,毕竟“空间”和“时间”都变化了,很多细节也要跟着变化。
凡事讲究从易到难,先挑一个简单的开整,就是这篇《Gold Price Prediction: Step By Step Guide Using Python Machine Learning》,作者是Ishan Shah 和 Rekhit Pachanekar,原文网址如下:
https://blog.quantinsti.com/gold-price-prediction-using-machine-learning-python/
其实这篇文章在翻译插件的帮助下,萌新想看明白也不难,其实就是讲了如何使用线性回归模型,根据两根均线的当前数值,预测黄金ETF第二天的价格,有代码有回测,最大的难点就是:代码跑不通!
为啥呢?因为里面使用了yfinance这个Python第三方库,它是基于雅虎(Yahoo)公开的API接口访问和获取黄金ETF的历史行情数据,但问题是这个库在2021年11月就停止了对中国的访问服务,要想正常使用,你要么在国外,要么自己搭梯子。
所以很多萌新发现自己跑不通文章上的代码,这是很正常的,在这里,咱用同样开源的akshare库替代yfinance,国内正常使用,还免费,一句话“pip install akshare”就可以安装了。
解决了数据获取这个最大的难题,接下来的事情就简单多了,按照原文的流程进行讲解,要想基于机器学习预测黄金ETF的价格,总共分为8步走。
Step1:导入Python库和读取黄金ETF数据
Import the libraries and read the Gold ETF data
首先,咱要导入建模和回测中所需要的全部Python库。
# 用于数据处理
import numpy as np
import pandas as pd
# 用于获取数据
import akshare as ak
# 导入线性回归模型
from sklearn.linear_model import LinearRegression
# 导入画图库、设置主题和中文显示
import matplotlib.pyplot as plt
plt.style.use('seaborn-darkgrid')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 中文显示
plt.rcParams['axes.unicode_minus'] = False # 负数显示
# 设置忽略警告
import warnings
warnings.filterwarnings('ignore')
from datetime import datetime接着要获取黄金ETF的数据,原文当中是获取SPDR黄金ETF从2018年1月1日至2020年6月22日的数据,为了本土化和与时俱进,将黄金ETF的品种改为我国上交所的黄金ETF(代码:518880),截止时间设为2024年5月17日,但由于它是在2013年7月才上市,所以起始时间设为2013年8月1日。
# 获取黄金ETF的历史行情数据
etf_data = ak.fund_etf_hist_em(symbol='518880', period='daily', start_date='20130801', end_date='20240517')
# 只需要收盘价序列
Df = etf_data[['收盘']].rename(columns={'收盘':'Close'})
# 将Index设置为datetime格式的日期
Df.index = pd.to_datetime(etf_data['日期']).tolist()
# 去除空值
Df = Df.dropna()
# 画出黄金ETF的价格走势图
Df.Close.plot(figsize=(15, 8), color='red')
plt.ylabel('黄金ETF价格')
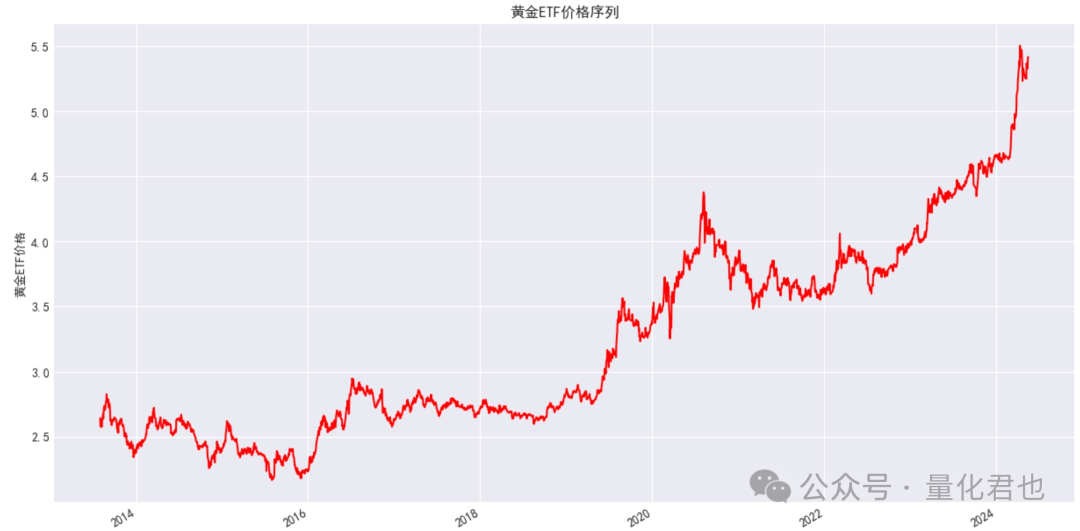
plt.title('黄金ETF价格序列')
plt.show()
# 查看Df的数据形式
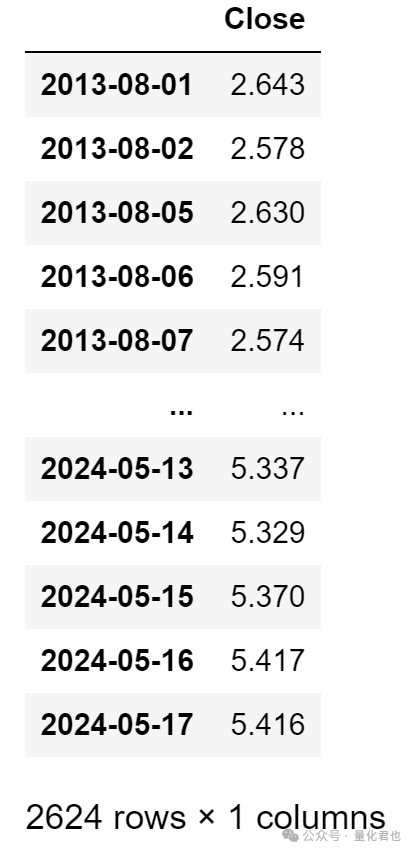
Df上面的代码是用akshare来获取黄金ETF的行情数据,只需要其中的收盘价序列,数据的形式是一个DataFrame,index为datetime格式的日期(与yfinance一致),columns只有一个收盘价(Close)字段,并画出黄金ETF收盘价序列。
上面代码的运行结果:
Step2:定义解释变量
Define explanatory variables
这一步要做的就是定义解释变量,简单来说,解释变量就是说你要用什么东西去预测黄金ETF的价格。其实解释变量在不同的领域还有不同的叫法,在数学领域叫做自变量,在机器学习领域叫特征,在量化领域叫因子,叫法不同,本质都是一个东西,就是y=f(x)当中的x,y就是你想预测的东西,比如说这里黄金ETF第二天的价格。
在这里,咱将使用55日移动均线和60日移动均线作为解释变量,你也可以根据自己的喜好加入更多的解释变量,比如说MACD、KDJ、RSI等等,这里咱保持原文当中两个均线因子的设定。
Step3:定义因变量
Define dependent variable
因变量就是咱要预测的目标,这里指的就是黄金ETF第二天的价格,更确切一点来说就是第二天的收盘价。
# 计算均线因子
Df['S1'] = Df['Close'].rolling(window=55).mean()
Df['S2'] = Df['Close'].rolling(window=60).mean()
# 第二天的收盘价
Df['next_day_price'] = Df['Close'].shift(-1)
Df = Df.dropna()
# 定义解释变量
X = Df[['S1', 'S2']]
# 定义因变量
y = Df['next_day_price']
X运行结果:
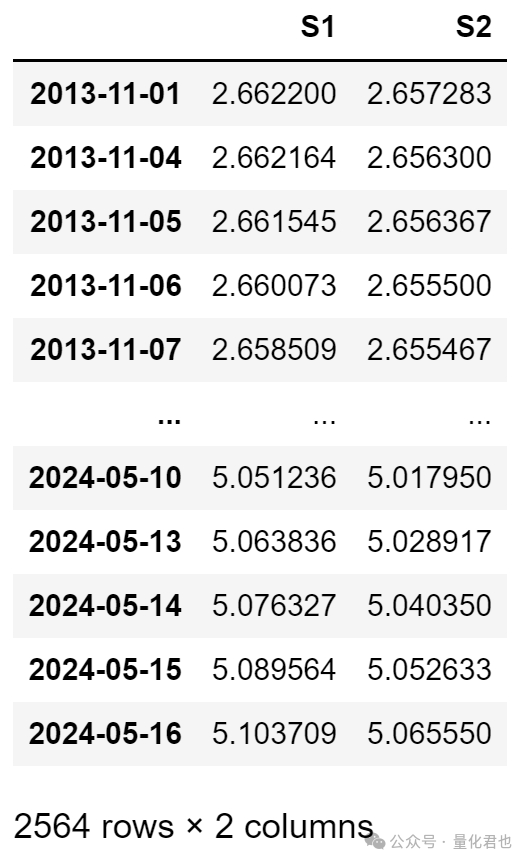
按照一般机器学习建模的命名规则,咱将解释变量的矩阵命名为X,格式为DataFrame,所以用大写的X,因变量只有一列数值,所以存储为Series格式,命名为小写的y。
Step4:将数据划分为训练集和测试集
Split the data into train and test dataset
这一步,咱就要将刚才的数据划分为训练集和测试集,训练集是用来训练模型的,也就是让机器学习模型自动拟合那两个均线因子与第二天收盘价的关系,测试集就是用来验证模型好坏的,验证好坏就是要用建模时没有出现过的数据,不然就跟高考全部用模拟考的题目,筛选出来的全都是些死记硬背的“人才”。
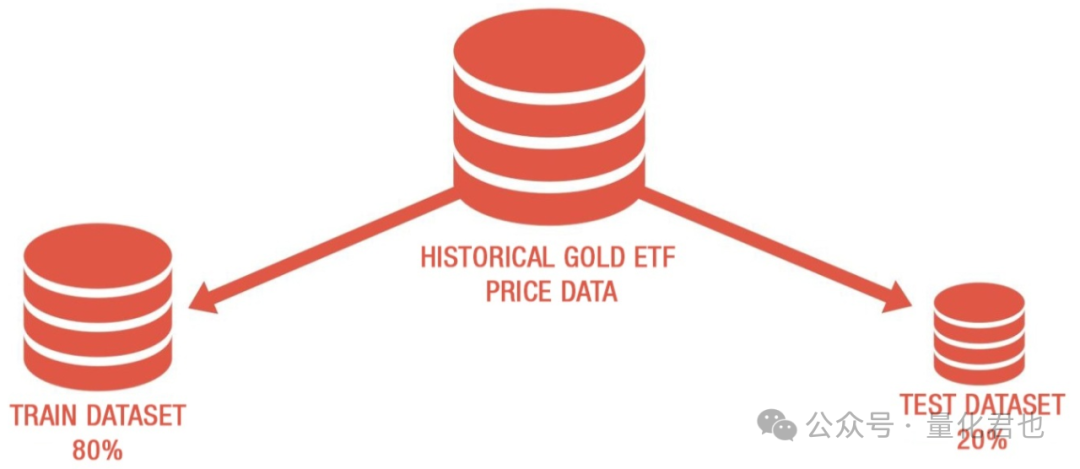
按照惯例,一般是将大部分数据用于训练模型,少部分数据用于验证模型,这里用80%的数据作为训练集,20%的数据作为测试集。下方代码中,X_train和y_train就是训练集数据,X_test和y_test就是测试集数据。
# 将数据划分为训练集和测试集
t = int(0.8 * Df.shape[0])
# 训练集
X_train = X.iloc[:t]
y_train = y.iloc[:t]
# 测试集
X_test = X.iloc[t:]
y_test = y.iloc[t:]
X_train运行结果:
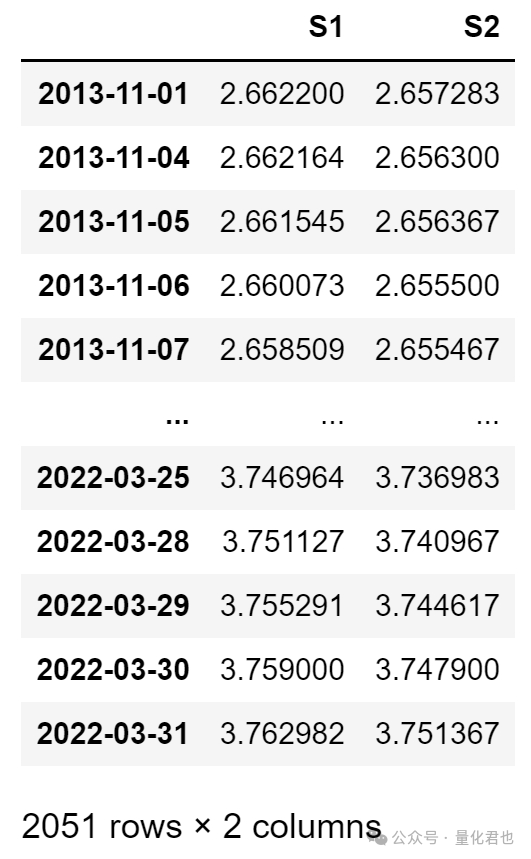
Step5:构建线性回归模型
Create a linear regression model
线性回归模型可以说是最常用的一种机器学习模型了,高中就接触过的最小二乘法OLS就属于线性回归。
线性回归基于一个或多个自变量预测因变量的值,它之所以被称为“线性”,那是因为它假设因变量和自变量之间的关系是线性的,形式如y=m1*x1+m2*x2+c,其中x1和x2是自变量,y是因变量,m1和m2就是回归系数,c又被称为截距或常数项。
# 创建线性回归模型并训练
linear = LinearRegression(fit_intercept=True).fit(X_train, y_train)
print('黄金ETF价格(y) = %.2f * 55日移动平均线(x1) \
%+.2f * 60日移动平均线(x2) \
%+.2f (constant)' %(linear.coef_[0], linear.coef_[1], linear.intercept_))运行结果:
黄金ETF价格(y) = 6.58 * 55日移动平均线(x1) -5.59 * 60日移动平均线(x2) +0.02 (constant)从运行结果中看出,线性回归模型基于训练集数据,学习到了回归系数和常数项分别是6.58、-5.59和0.02,那么整个模型就可以表示为:
黄金ETF价格 = 6.58 * 55日移动平均线 - 5.59 * 60日移动平均线 + 0.02
注意,这里的均线值是今日的,黄金ETF价格是预测第二天的。
Step6:预测黄金ETF价格
Predict the Gold ETF prices
上一步模型训练好了,那咱就可以预测黄金ETF的价格了,直接调用LinearRegression对象当中的predict函数就可以预测了(sklearn库当中的模型都可以这样操作)。
# 预测黄金ETF第二日的价格
predicted_price = linear.predict(X_test)
predicted_price = pd.DataFrame(predicted_price, index=y_test.index, columns=['price'])
predicted_price.plot(figsize=(15, 8))
y_test.plot()
plt.legend(['预测的价格', '实际的价格'])
plt.ylabel('黄金ETF的价格')
plt.show()运行结果:
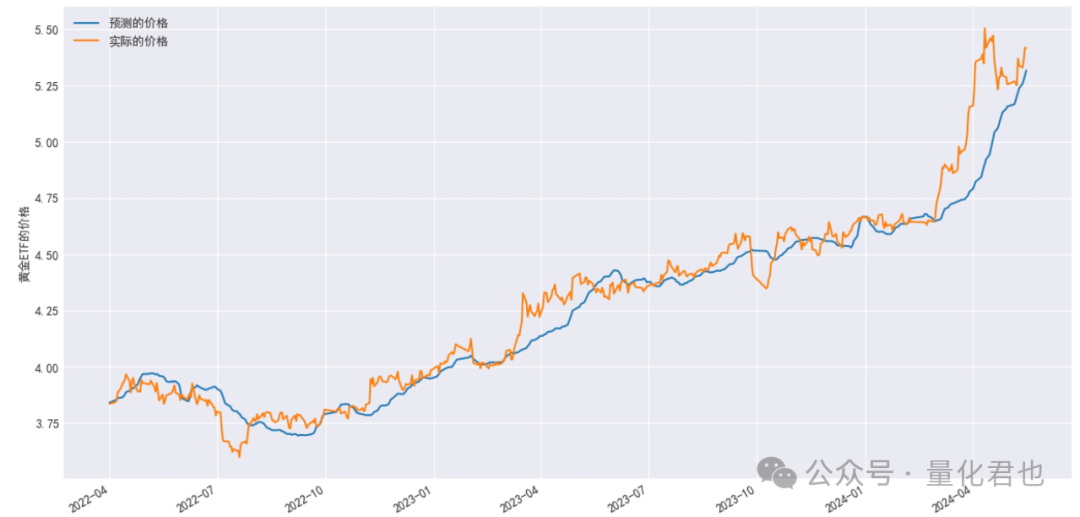
上图当中的黄线是黄金ETF实际的价格,蓝线是预测的价格,预测值对实际值还是跟踪得比较紧密的,那有什么指标定量去衡量它们之间的拟合程度呢?
那就是决定系数R2了,坊间一般称为“R方”,计算公式如下。
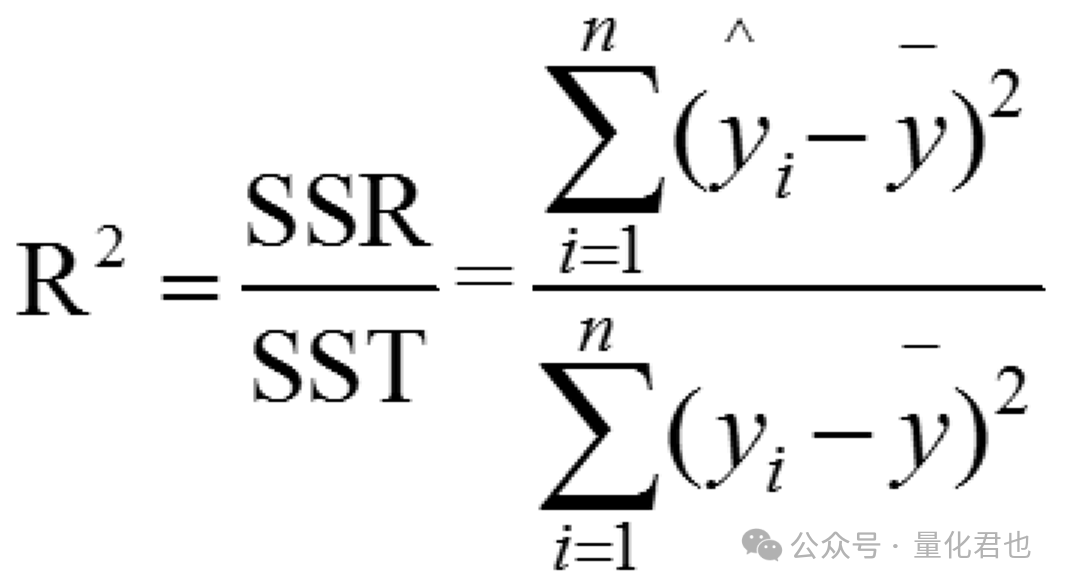
其中,y是真实值,y横线是平均值,y三角是预测值。决定系数R2的取值范围一般在0~1之间,数值越大,表示线性拟合的效果就越好,当直线能完美拟合所有数据点时,取值为1。
要计算决定系数R2也非常简单,直接调用LinearRegression对象当中的的score函数就可以了。
# 决定系数R2
r2_train = linear.score(X_train, y_train)
r2_test = linear.score(X_test, y_test)
print('训练集决定系数: %.4f' %r2_train)
print('测试集决定系数: %.4f' %r2_test)运行结果:
训练集决定系数: 0.9712
测试集决定系数: 0.9301可以看到,训练集和测试集的模型决定系数R2分别是0.9712和0.9301,跟天花板1.0比较接近,属于不错的拟合效果,训练集拟合效果更好的原因也不言而喻,对训练过程中就出现过的样本数据当然拟合效果更好,对从未谋面的测试集数据拟合效果好才是真本事。
Step7:回测并绘制累积回报图
Backtesting and plotting cumulative returns
模型建好了,并且对已知数据和未知数据的拟合效果都还行,那就基于这个模型构建一个黄金ETF的交易策略,核心交易逻辑是:如果模型预测的黄金ETF价格比前一个预测值高,则买入黄金ETF,否则,卖出黄金ETF或空仓不操作。
在具体实现当中,今天的predicted_price_next_day对应的是明天黄金ETF价格的预测值,如果这个值比昨天预测的值高,那么交易信号signal记为1,否则signal记为0,那怎么计算策略的收益率和净值呢?
那首先要计算出黄金ETF的日收益率序列,当今日signal为1时,对应的是第二日有持仓,当signal为0时,对应的是第二日没有仓位,假设每次都是满仓交易,那只要将有持仓的黄金ETF日收益率纳入作为策略的日收益就可以了,其他时间策略的日收益率为0,有了策略的日收益率序列后,只要做一个简单的连乘操作就可以算出净值曲线了,具体实现代码如下所示。
# 只考虑测试集当中的数据
gold = pd.DataFrame()
gold['price'] = Df.iloc[t:]['Close']
gold['predicted_price_next_day'] = predicted_price
# 黄金ETF的日收益率
gold['gold_returns'] = gold['price'].pct_change()
# 如果预测价格比前一个预测的价格高,则买入,否则卖出或空仓
gold['signal'] = np.where(gold.predicted_price_next_day.shift(1) < gold.predicted_price_next_day, 1, 0)
# 策略的日收益率
gold['strategy_returns'] = gold['signal'].shift(1) * gold['gold_returns']
# 策略和基准的净值曲线
gold['strategy_nv'] = (gold['strategy_returns'] + 1).cumprod()
gold['bmk_nv'] = (gold['gold_returns'] + 1).cumprod()
# 绘制净值曲线图
gold[['strategy_nv','bmk_nv']].plot(figsize=(15, 8), color=['SteelBlue', 'Yellow'],
title='黄金ETF价格择时策略净值曲线图 by 公众号【量化君也】')
plt.legend(['策略净值', '基准净值'])
plt.ylabel('净值')
plt.show()运行结果:
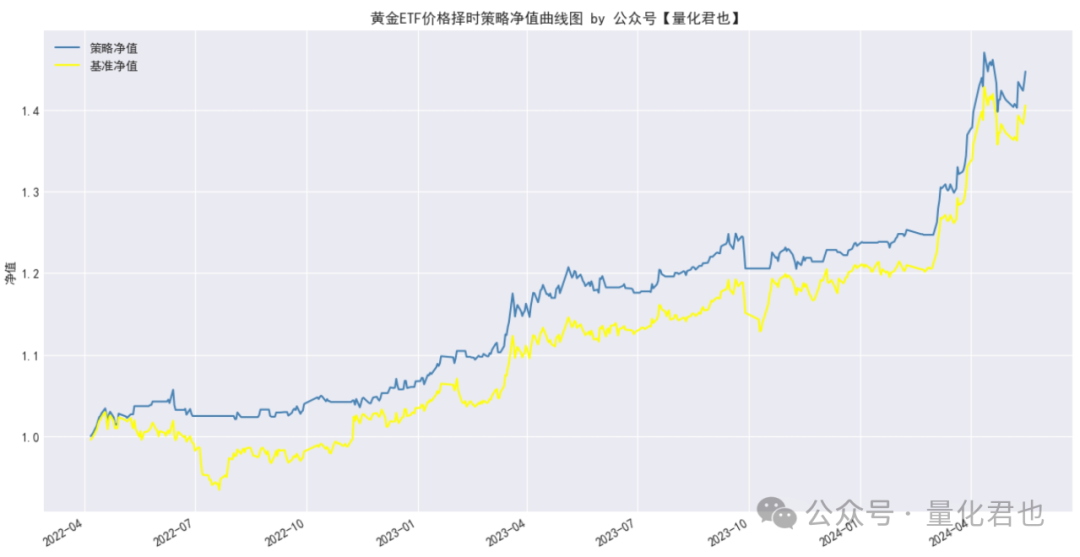
可以看到,策略净值曲线在基准净值曲线(买入并一直持有黄金ETF)之上,说明择时的效果比Buy & Hold要好一些,并且在大跌前基本都会卖出空仓,持有体验也会好一些。
接着咱再来计算一下策略和基准的夏普率,策略的夏普率是2.14,基准的是1.66,定量表明在风险调整后的收益方面,策略也是跑赢基准的。
# 计算夏普率
strategy_sharpe = gold['strategy_returns'].mean() / gold['strategy_returns'].std() * (252**0.5)
bmk_sharpe = gold['gold_returns'].mean() / gold['gold_returns'].std() * (252**0.5)
print('策略夏普率: %.2f' %strategy_sharpe)
print('基准夏普率: %.2f' %bmk_sharpe)输出结果:
策略夏普率: 2.14
基准夏普率: 1.66Step8:每日滚动预测
Using this model to predict daily moves
当你确认这个模型可用之后,以后日常就是每天来看一下明天的预测值是多少,对应的交易操作是什么。
有了前面的铺垫,要实现这个功能就很简单了,只要将训练好的模型保存下来,每日获取近期的黄金ETF数据塞进模型里面预测,然后把最新的一行打印出来就可以了,实现代码如下。
# 当前日期
current_date = datetime.now().strftime('%Y%m%d')
# 获取数据
etf_data = ak.fund_etf_hist_em(symbol='518880', period='daily', start_date='20230101', end_date=current_date)
data = etf_data[['收盘']].rename(columns={'收盘':'Close'})
data.index = pd.to_datetime(etf_data['日期']).tolist()
# 计算均线因子
data['S1'] = data['Close'].rolling(window=55).mean()
data['S2'] = data['Close'].rolling(window=60).mean()
data = data.dropna()
# 预测黄金ETF第二天的价格
data['predicted_gold_price'] = linear.predict(data[['S1', 'S2']])
data['signal'] = np.where(data.predicted_gold_price.shift(1) < data.predicted_gold_price, '买入' , '空仓')
# 输出预测值
data.tail(1)[['signal','predicted_gold_price']].T运行结果:

看到这里,你应该对用机器学习算法构建量化交易策略,有了一个框架性的了解,后面要精进的话,最主要的就是选入更多的因子(解释变量)和选用更高级的机器学习算法,基本的框架流程大抵还是这样,建议结合原文和本文对照阅读,这样就会发现一些有趣的细节改动。
终于吭哧吭哧写完了,下期见~
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
